<img style="width: 1046px;" data-filename="intro_machine_learning_1.jpeg" src="/uploads/tutorials/2020/07/21_intro_machine_learning_1.jpeg"> We are now living in the age of data. Every day we are producing immense data you can not even think of! According to some statistics, we are producing 2.5 quintillions bytes of data every day. See! This is huge and here comes the necessity of data-driven applications or precisely Machine Learning. As we have so much data around us we can find valuable insights and patterns from the data. And machine learning helps us to do so.
Around the year's machine learning has become a buzzword in the software industry and everyone is trying to make some use of machine learning to get more benefits from data. Google uses it to make the search more personalized, Amazon uses it to understand customer behavior, Facebook uses to face recognition and almost every giant company consider it seriously.
So, let's dive into the basic aspects of machine learning. This tutorial is developed to teach you all the concepts and phenomena you need to know about machine learning in the first place.
<h4>What Is Machine Learning?</h4>
Machine Learning(ML) is a subset of artificial intelligence where algorithms are developed to learn through experience from data. Machine Learning algorithms differ from traditional computer algorithms in their approach. Traditional computer algorithms are developed to perform a set of well-defined tasks where every instruction is defined properly and the algorithm is evaluated against the expected result. Whereas ML algorithms are developed to analyze data, learn from the data, and predict a result according to its learning experience. Here the approach is more statistical than explicitly programmed like traditional computer programs.
In brief, Machine learning is a subset of artificial intelligence that automates an analytical model built by using an algorithm that iteratively learns from data without being explicitly programmed. A system to ask questions and answers.
<h4>How Do Machine Learning Algorithms Work?</h4>
Machine learning algorithms are sophisticated mathematical models based on sample data. The data is mostly divided into two parts- training and evaluation/test data. The training data is fed to the mathematical model. The model then analyzes the mathematical properties among different attributes(here, attributes are the various aspects of data) and try to find some patterns/relationships among them. This is the learning part of a model.
Then come to the result part, here the model has to predict some output based on its learning. The model tries to fit the experience it has gain from the training data to an unknown situation and predicts according to its previous experience. The performance of the model is evaluated against the evaluation/test data. The accuracy of the model is taken as a percentage of how much it could predict accurately.
Take a traditional example from your mailbox. There are some messages which are kept in the spam folder. Spam messages are those which contain misleading information or inappropriate messages. So, how do the mails are classified as spam or not spam? Well, there is a simple machine learning concept behind this. Every spam emails contain some common words. The idea is here to remember those words and every time they are seen as a decent percentage then the email will be classified as spam. Here the model tries to find the percentage of those word from its previous experience which is gained from a set of training data containing emails labeled as "spam" and "not spam"
<h4>Examples of Machine Learning Applications in Real Life</h4>There are numerous examples of machine learning in our day to day life. And the number of machine learning applications is increasing day by day. Here some of the common applications-1. Image Recognition Have you ever think about how Facebook or other social media tag people in a picture? Right! They use machine learning, specifically image recognition. It is an area of machine learning where a mathematical model is fed with image data with appropriate labels, the model learns from the image features and then tries to classify from this experience. 2. Conversational Intelligence Softwares Siri, Alexa, Google Assistant, and other voice assistants are good examples of conversational AI Softwares. And they use similar concepts form Natural Language Processing and Machine Learning to incorporate the human voice with intelligence. 3. Product Recommendation The wide use of machine learning is recommendation engines. There are many examples of them such as Amazon uses it to suggest similar products from your previous purchases. Netflix uses it to recommend movies of your choice. Here the model analyzes the user behavior, continuously learns from it, and predicts according to its experience. 4. Personalized Advertisements Probably the biggest use of machine learning is in personalized advertisements. A model learns from a user behavior- from search history, buying pattern, liked products in social media, etc. and then it adjusts the choice of a user with an appropriate ad. All the technology giants like Google, Facebook, and other social media use this type of model to advertise their users. 5. Healthcare Machine learning tools and algorithms are massively used in disease diagnosis. There are also uses in drug designing, genome sequencing, and many other healthcare issues.<h4>Types of Machine Learning Algorithms</h4>Basically, there are three types of machine learning algorithms-













<ul><li>Supervised Learning</li>
 <li>Unsupervised Learning</li>
 <li>Reinforcement Learning</li></ul><img data-filename="22_intro_machine_learning_1.png" style="width: 899px;" src="/uploads/tutorials/2020/07/1595341855_21_22_intro_machine_learning_1.png"> <ul></ul>These three types are then extended into more classifications. Let's take some overviews of those types.
<h5>Supervised Learning Algorithms</h5>
As the name suggests, the model gets some guidance or supervision in the time of training. It deals with labeled data or more precisely the model knows about the output while it is being trained. In a supervised learning approach, the data variables are divided into dependent and independent variables. Here dependent variable(s) are the outputs with an explicit label(i.e. yes/no or a specific value). The model tries to find the correlation between the dependent and independent variables and use this knowledge to predict the outcome.
Recall our previous example of the classification of emails. When the model is in training, the emails are fed with labels as "spam" or "not spam". This is a supervised learning algorithm.<img style="width: 977px;" data-filename="intro_machine_learning_3.png" src="/uploads/tutorials/2020/07/21_intro_machine_learning_3.png"> 
Supervised Learning has two types-
<ul><li>Regression Regression is used when the output label is a continuous value such as money, age, weight where the model has to predict a value in some sort of range.&nbsp;For example, if you have a dataset that contains the salary of a certain number of employees according to their experience, your model will find the correlation between the experience and salary from that dataset. And with that experience, it will predict the unknown salary of employees from their experience.&nbsp;Here, salary is a continuous variable.</li>
 <li>Classification&nbsp;Classification is the task of predicting the value of a categorical variable(target or class). Here, the output is discrete. The model has to classify the classes. For instance, if you have a dataset that represents the status of the customer whether they buy a certain product or not. This is a problem to be solved by a classification model.</li>
</ul><h5>Unsupervised Learning Algorithms</h5>
Unsupervised learning deals with unlabeled data. Here the model does not the output in the time of training. The model has to analyze the data, finds some patterns from them, and act according to its learning. This is more like feeding the model a set of data from which we need to find some insight but don't know how to get that. So, we let it to an unsupervised mode. The model can discover something we have not thought before!<img style="width: 946px;" data-filename="intro_machine_learning_4.png" src="/uploads/tutorials/2020/07/21_intro_machine_learning_4.png"> 
Unsupervised learning has two type-
<ul><li>Clustering This is basically analyzing the data to group them to some clusters based on similarity among the data. Here, the groups are made from the data which are similar in nature(statistically of course!). An example can be taken as grouping customers according to their expenditure (i.e. small, medium, big). Here we did not classify them before. The model will do that.</li>
 <li>Association Association algorithms try to find some rules or associations among the data. The model relates a data point to another with a rule it has discovered by analyzing the dataset. You may have seen this in various e-commerce sites like Amazon. When you go there to buy a product there is a section named frequently bought together or people also buy this comes up and prompts you similar products to buy.</li>
</ul><h5>Reinforcement Learning</h5>
Reinforcement Learning is reward-based learning. The algorithm or agent learns from its surrounded environment. The environment contains rewards and penalties. The model performs various actions. It receives rewards for correct actions and gets penalties for improper actions. The model is defined as to maximize its rewards and minimize its penalties. It always tries to leverage itself from previous experience i.e. tries not to repeat a wrong action again or do a correct action every time. This is a dynamic learning environment where the agent needs to respond correctly with his action.&nbsp;
Think of a computer program that solves a maze. First, it makes many mistakes. But it improves after every decision it takes. Repeating the actions continuously, it eventually becomes a better player. This is a simple example of reinforcement learning.<img style="width: 977px;" data-filename="Machine-Learning-Explained3.png" src="/uploads/tutorials/2020/07/21_Machine-Learning-Explained3.png"><h4>Final Thoughts</h4>In this article, I have tried to keep you informed about the main aspects of machine learning. I started with the definition and use cases of machine learning then went further to give you some glimpses of how machine learning works. I tried to give you a clear idea about the different types of machine learning algorithms and their example uses.&nbsp;The possibilities of using machine learning in various fields are increasing day by day. If you become a data scientist/ML engineer, it is high time you should learning machine learning algorithms.&nbsp;Hope this article provided you enough ideas to kickstart your journey. Happy Machine Learning!

An Introduction to Machine Learning | The Complete Guide

<img data-filename="data-preprocessing-with-python.png" style="width: 600px;" src="/uploads/tutorials/2020/08/10_data-preprocessing-with-python.png"> Data Preprocessing: Data Prepossessing is the first stage of building a machine learning model. It involves transforming raw data into an understandable format for analysis by a machine learning model. It is a crucial stage and should be done properly. A well-prepared dataset will give the best prediction by the model.
Why Data Preprocessing is so Important?
<ul><li>Raw data may contain improper values or in an incorrect format.</li>
 <li>Making the dataset feasible for the analysis.</li>
 <li>For achieving the best result from a dataset.</li>
 <li>Quality result depends on quality data. I.e. improper or missing data can lead a model to give confusing output</li>
</ul>Major tasks in Data Preprocessing: The major tasks in Data Preprocessing are given below:
1.Data cleaning: Fill in missing values, smooth noisy data, identify or remove outliers, and resolve inconsistencies.
2.Data Integration: Integration of multiple databases, data cubes, or files.
3.Data Transformation: Normalization and aggregation.
4.Data reduction: Reduced representation in volume but produces the same or similar analytical results.
5.Data discretization: Part of data reduction but with particular importance, especially for numerical data.
Important: We will use the Spyder IDE from Anaconda for executing the codes. To start with executing the following codes in Spyder, first, you need to set the folder where you keep this dataset as the working directory. To do so, you need to go to the file explorer of your Spyder IDE and set the folder as the working directory.<img data-filename="1_Data_Preprocessing (2).jpg" style="width: 1046px;" src="/uploads/tutorials/2019/05/28_1_Data_Preprocessing_(2).jpg"> 
Then for executing the code given here, you need to write them on the Spyder editor. After that, you need to select all the code and press ctrl+enter(in windows). Then you will see the output on the IPython console.<div><img data-filename="2_Data_Preprocessing_Spyder.png" style="width: 1046px;" src="/uploads/tutorials/2019/05/28_2_Data_Preprocessing_Spyder.png"></div><div> You can see the variables from the variable explorer. <div><img data-filename="3_Data_Preprocessing.jpg" style="width: 1046px;" src="/uploads/tutorials/2019/05/28_3_Data_Preprocessing.jpg"> </div></div> In this tutorial, I will show you how to pre-process your data using several techniques.
&nbsp;
Getting the Dataset: There are several places from where you can download standard datasets. Kaggle is the best place for that. You can also get data from UCI machine learning database, data.gov, and google public dataset. For this tutorial, I used this dataset named Data.csv.&nbsp; You can download it from <a href="https://www.dropbox.com/s/1gx66hwxih5xy13/Data.csv?dl=0">here</a>.&nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp;&nbsp;<img data-filename="1_Dataset_Image.png" style="width: 292px;" src="/uploads/tutorials/2019/05/28_1_Dataset_Image.png"> 
Importing the Libraries: Libraries are tools in python that we can use to make a specific job. And what's cool about these libraries is that you just have to give some inputs and the library will do the rest of the job. For making our models we are going to use a lot of libraries but there are three most common libraries that are used in every program. So, first of all, we will import those libraries. You will get the full code in <a href="https://colab.research.google.com/drive/1WmhGoDIhGgajtmH7DRprCLrerxlAE8e2?usp=sharing" target="_blank">Google Colab</a>. Now let's get into the work.
<pre>import numpy as np import matplotlib.pyplot as plt import pandas as pd
</pre>Here, the library numpy contains lots of predefined tools to do mathematical and scientific operations on the data. matpolotlib.pyplot is the library to plot the data in charts. And the last one, pandas provides tools to read and import the dataset.Importing the Dataset: First, we import the dataset from our working directory. For this, we need to do the following:<pre>dataset = pd.read_csv('Data.csv')
</pre>Note: The dataset must be in CSV format.
There is something you must understand in machine learning is that in Python, we need to distinguish the matrix of feature and the dependent variable vector in our dataset. The independent variables which are used to predict the value of the dependent variable are contained in the Feature Matrix. The dependent variable is kept in the dependent variable vector. If you look back into the dataset you can see that the first three columns- States, Age, Salary are independent variables that we must take in the feature matrix. Let's denote it as X. And then we take the Purchased column in the dependent variable matrix, denoting y. The codes are as follows:<pre>X = dataset.iloc[:, [0,1,2]].values
y = dataset.iloc[:, 3].values </pre>The output for X should be like this: <pre>array([['Texas', 44.0, 72000.0], ['Florida', 27.0, 48000.0], ['California', 30.0, 54000.0], ['Texas', 38.0, 61000.0], ['California', nan, 65000.0], ['Texas', 35.0, 58000.0], ['California', 40.0, nan], ['Texas', 48.0, 79000.0], ['Florida', 50.0, 83000.0], ['Texas', 37.0, 67000.0]], dtype=object)
</pre>And for y it will be:<pre>array(['No', 'Yes', 'No', 'No', 'Yes', 'Yes', 'No', 'Yes', 'No', 'Yes'], dtype=object)
</pre>Handle the Missing Data: If you look into the dataset you should find that there are some missing values in age and salary columns(actually it's two, one in the Age column and another in the&nbsp;Salary column). This missing data will cause irregularities in our machine learning model. So we need to handle these missing data. For this, we use&nbsp;SimpleImputer&nbsp;class from the Scikit-learn library of Python. There are many strategies to handle missing data, we can take the average or median or mean of the column. Here we will take the median value.&nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp;&nbsp;<img data-filename="6_Data_Preprocessing.jpg" style="width: 513px;" src="/uploads/tutorials/2019/05/28_6_Data_Preprocessing.jpg"> 
Handling the missing values<pre style="margin-bottom: 14px; padding: 9px 14px; border-color: rgb(225, 225, 232);">from sklearn.impute import SimpleImputer
imputer = SimpleImputer(missing_values=np.nan, strategy='mean')
imputer.fit(X[:, 1:3])
X[:, 1:3] = imputer.transform(X[:, 1:3])</pre>Note: Python uses 'NaN' to represent missing values.
The output should look like this:<pre style="margin-bottom: 14px; padding: 9px 14px; border-color: rgb(225, 225, 232);">array([['Texas', 44.0, 72000.0],
['Florida', 27.0, 48000.0],
['California', 30.0, 54000.0],
['Texas', 38.0, 61000.0],
['California', 38.77777777777778, 65000.0],
['Texas', 35.0, 58000.0],
['California', 40.0, 65222.22222222222],
['Texas', 48.0, 79000.0],
['Florida', 50.0, 83000.0],
['Texas', 37.0, 67000.0]], dtype=object)</pre>Here the missing values are replaced by the mean of the respective column values(highlighted in yellow).
Categorical Data: In our dataset, we have two columns- States and Purchased, both containing categorical data. These two variables are categorical variables because simply they contain categories(i.e. name of a state, or yes/no values). Since machine learning models are based on mathematical equations, you can intuitively understand that they would not fit in our model well. So, we can not keep the categorical variables because we only can use numbers in the equations.
That's why we need to encode the categorical variables.<pre style="margin-bottom: 14px; padding: 9px 14px; border-color: rgb(225, 225, 232);">#Encoding the categorical variables
from sklearn.preprocessing import LabelEncoder, OneHotEncoder
from sklearn.compose import ColumnTransformer
labelencoder_X = LabelEncoder()
X[:, 0] = labelencoder_X.fit_transform(X[:, 0])
labelencoder_y = LabelEncoder()
y = labelencoder_y.fit_transform(y)
y = y.reshape(-1, 1)</pre>Note: here, LabelEncoder&nbsp;converts the categorical values into numbers so that they could be used in the machine learning equation.The outputs are-
For X:<pre style="margin-bottom: 14px; padding: 9px 14px; border-color: rgb(225, 225, 232);">array([[2, 44.0, 72000.0],
[1, 27.0, 48000.0],
[0, 30.0, 54000.0],
[2, 38.0, 61000.0],
[0, 38.77777777777778, 65000.0],
[2, 35.0, 58000.0],
[0, 40.0, 65222.22222222222],
[2, 48.0, 79000.0],
[1, 50.0, 83000.0],
[2, 37.0, 67000.0]], dtype=object)</pre>For y:<pre style="margin-bottom: 14px; padding: 9px 14px; border-color: rgb(225, 225, 232);">array([0, 1, 0, 0, 1, 1, 0, 1, 0, 1])</pre>&nbsp;At the output, for X the values for the&nbsp;States column and for y, the values for the Purchased column are replaced by numbers.
Note: Though categorical values are converted to numbers, they will still cause a problem. You can observe that the encoding has made one state having a higher or lower value than others. As a machine learning model is based on equations, the numbers denoting the states will have some effect on the equation(i.e. persons from a higher/lower value state may be predicted to have a higher/lower salary than persons from other states). But this is not the thing we wanted, these are actually categorical data with no relational order between them. To solve this problem, we need to make dummy variables so that our machine learning model does not confuse with the weight of the categorical values. The following code will generate a dummy variable for each of the three states contained in our dataset.<pre style="margin-bottom: 14px; padding: 9px 14px; border-color: rgb(225, 225, 232);">#Creating dummy variables for the encoded categorical values
transformer = ColumnTransformer([('one_hot_encoder', OneHotEncoder(), [0])],remainder='passthrough')
X = np.array(transformer.fit_transform(X), dtype=np.float)
</pre>After creating dummy variables the X dataset should look like:
&nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp;&nbsp;<img src="/uploads/tutorials/2019/05/23_1_Salary_Datset.png" alt="23_1_Salary_Datset"> 
Here columns 0, 1, and 2 represent dummy variables for the three categorical values.
We need not make dummy variables for y dataset. Since this is the dependent variable and our machine learning model knows it is a category and that there is no order between the two(yes/no) values. So, LabelEncoder will do good enough for the y dataset.
Splitting the dataset: Now, we need to split the dataset into training and test dataset. The training dataset is used to train the machine learning model and the test dataset is to test the model.<pre style="margin-bottom: 14px; padding: 9px 14px; border-color: rgb(225, 225, 232);">#Splitting the datasets
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.2, random_state = 0 )</pre>
Note:&nbsp;Here, test_size = 0.2 means we take 20% of our data to the test set, and the remaining 80% will be in the training set. random_state = 0 is to ensure that after splitting, your datasets and our dataset look become the same.After splitting the dataset should look like this:
&nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp;&nbsp;<img src="/uploads/tutorials/2019/05/23_2_X_Train_Numpy_Array.png" alt="23_2_X_Train_Numpy_Array"> 
 
&nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp;<img src="/uploads/tutorials/2019/05/23_3_X_Test.png" alt="23_3_X_Test"> 
 
&nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp;<img src="/uploads/tutorials/2019/05/23_4_Y_Train_Numpy_Array.png" alt="23_4_Y_Train_Numpy_Array">
 
&nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp;<img src="/uploads/tutorials/2019/05/23_5_Y_Test_Numpy_Array.png" alt="23_5_Y_Test_Numpy_Array"> 
&nbsp;
Feature Scaling: Now, we come to the last part of preprocessing. Let's explain what is features scaling and why we need to do it.
If you look at the dataset again, you can see the two columns namely Age and Salary contain numerical data. You should notice that the variables are not on the same scale. The Age is going from 27 to 50 while the Salary has a range of 48000 to 83000. And there is no distinguished linear relationship between these two columns.&nbsp; This will cause inaccurate predictions by our model. So we need to scale them to get a more accurate prediction from the model.<pre style="margin-bottom: 14px; padding: 9px 14px; border-color: rgb(225, 225, 232);"># Feature Scaling
from sklearn.preprocessing import StandardScaler
sc_X = StandardScaler()
X_train = sc_X.fit_transform(X_train)
X_test = sc_X.transform(X_test)
sc_y = StandardScaler()
y_train = sc_y.fit_transform(y_train)</pre>&nbsp;After feature scaling the dataset will look like the following: &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp;<img data-filename="7_X_Train_Feature_Scalling.png" style="width: 548px;" src="/uploads/tutorials/2019/05/28_7_X_Train_Feature_Scalling.png">&nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp;<img data-filename="8_X_test_Feature_Scalling.png" style="width: 542px;" src="/uploads/tutorials/2019/05/28_8_X_test_Feature_Scalling.png">&nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp;&nbsp;<img data-filename="10_y_train_Feature_Scalling.png" style="width: 151px;" src="/uploads/tutorials/2019/05/28_10_y_train_Feature_Scalling.png">Data preprocessing is the fundamental step to start creating a model, we will go further and see how the machine learning model is built using various algorithms and techniques in the following articles.

Data Preprocessing for Machine Learning | Apply All the Steps in Python

Regression: Basically, Regression is a statistical approach to find the correlations between variables(dependent and independent).
In the context of machine learning, Regression is an algorithm or technique that is applied to a certain dataset to find the correlation between the independent and dependent variables and with that, predicts the&nbsp;outcome of an unknown value.
For example, if you have a dataset that contains the salary of a certain number of employees according to their experience, your model will find the correlation between the experience and salary from that dataset. And with that correlation, it predicts the unknown salary of employees from their experience.
How Does It Work?
Let's take an example of a regression task. Assume that we have a dataset that contains the price(in dollars) of houses according to their area(in meter squared) of the town Branalle. The plot for price vs area data of the town Branalle is depicted below:
&nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp;<img src="/uploads/tutorials/2018/09/18_regression_1.png" alt="18_regression_1"> 
Here the value of area on the X-axis is the independent variable, and on the Y-axis, the value of the price is the dependent variable.
Now if we build a regression model based on this data, our model will try to find the correlation between the area and the price. And from that correlation, the outcome of the model will be a simple line(linear or nonlinear based on the chosen algorithm) on the graph. The line will be the prediction line of the model, upon which it will predict the unknown price according to the given area of a house.
&nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp;&nbsp;<img src="/uploads/tutorials/2018/09/18_regression_2.png" alt="18_regression_2"> 
Here the line is the prediction line constructed by the regression model. This prediction line will be used as a reference to predict an unknown value, that is the price of a house.
How to Understand a Regression Task?
Regression algorithms give you a continuous output. That means if you are asked to build a model that predicts the future outcome where the output will be continuous. Then you must choose one of the Regression algorithms to build your model.
For example, if you are provided with a dataset about houses, and asked to predict their prices, that is a regression task because the price will be a continuous output.
Classification of Regression:
There are several types of Regression models. They are as follows:
<ul><li>
 <a href="http://www.aionlinecourse.com/tutorial/machine-learning/simple-linear-regression">Simple Linear Regression</a>
 </li>
 <li>
 <a href="http://www.aionlinecourse.com/tutorial/machine-learning/multiple-linear-regression">Multiple Linear Regression</a>
 </li>
 <li>
 <a href="http://www.aionlinecourse.com/tutorial/machine-learning/polynomial-regression" target="_blank">Polynomial Regression</a>
 </li>
 <li>
 <a href="http://www.aionlinecourse.com/tutorial/machine-learning/support-vector-regression" target="_blank">Support Vector Regression </a></li><li><a href="http://www.aionlinecourse.com/tutorial/machine-learning/decision-tree-intuition" target="_blank">Decision Tree Regression</a>
 </li>
 <li>
 <a href="http://www.aionlinecourse.com/tutorial/machine-learning/random-forest-regression" target="_blank">Random Forest Regression</a>
 </li>
</ul>In the following articles, we will understand these models in detail and learn how to implement them in Python.
&nbsp;
&nbsp;

Regression

<img style="width: 1046px;" data-filename="Two-birds-European-bee-eater_1920x1440.jpg" src="/uploads/tutorials/2020/07/22_Two-birds-European-bee-eater_1920x1440.jpg"> Regression models try to fit the best line to a set of observed data points. While simple linear models use a straight line, other models like multiple regression or polynomial regression use curved lines. A regressive model allows you to understand how the dependent variable changes in response to the change of independent variables.In this tutorial, we are going to understand what is simple linear regression. We will then implement a simple linear regression model in python. So, stay tuned!<h4>What is Simple Linear Regression?</h4>A simple linear regression model only has two explanatory variables- one dependent and one independent variable. Think of a two-dimensional space where the horizontal axis represents the independent variable x, and the vertical axis represents the dependent variable y. Like that, a simple linear regression model uses two-dimensional sample points.&nbsp;The model predicts the values of the dependent variable as a function of the independent variable.&nbsp;It tries to find a simple linear function that represents the relationship between the independent and the dependent variable as accurately as possible. The function simply creates a straight line, more specifically a slope that resembles the prediction line.&nbsp;For example, there is a relationship between cigarette consumption and cancer. More consumption of cigarettes creates a high chance of cancer. The relationship here seems linear and the variables can be fitted in a two-dimensional space. So, we can describe this phenomenon using a simple linear regression model.<h4>The Formula for Simple Linear Regression Model</h4>The formula representing a simple linear regression is-<pre>y = b0 + b1X + e
</pre>Let's interpret the equation<ul><li>y represents the predicted value of the dependent variable according to the given value of the independent variable.</li><li>b0 represents the intercept, the value of the function when the independent variable is 0</li><li>b1 is the regression coefficient, it tells how much the values of the function will scale to the independent variable</li><li>X represents the independent variable of the function&nbsp;</li><li>e represents error the model is creating</li></ul>With this function, a simple linear regression model will predict the dependent variable(denoted y) values as a function of the independent variables(denoted x). Basically, this function generates a straight line in the cartesian coordinate system. This straight line is the prediction line for the simple linear regression model which tries to predict the dependent values as accurately as possible.<h4>Assumptions of Simple Linear Regression</h4>Simple linear regression model uses a parametric test. The parametric test depends on the distribution of the data(often normal distribution). So it makes some certain assumptions about the data. There are four assumptions associated with a simple linear regression model-&nbsp;<ul><li>Linearity It assumes that the relation between the data points is linear i.e. the plot of the data points shows is linear</li><li>Independence There must be no relationship among the different values of the independent variable i.e. the value is unique</li><li>Normality Data points follow a normal distribution i.e. if we plot the histogram of the data, we should be able to draw a skewed line</li><li>Equal Variance The variance of the data should be equally distributed i.e. they do not "fan-out" in a triangular fashion</li></ul>When your data does not meet any of the above assumptions you can not perform a simple linear regression. Rather you should use a nonparametric test.Think about stock price data. Here observations for the same entity(stock) are collected over time. This data violates the assumption of independence and the data is also not linear. So, we can not perform linear regression on this data.<h4>Simple Linear Regression in Python</h4>There is a simple and easy way to build a simple linear regression model. In this tutorial, we will use the Scikit-learn module to perform simple linear regression on a data set.
We take a salary dataset. It has two variables- years of experience and salary. Therefore, the data set is two-dimensional. Taking the experience as the independent variable and the salary as the dependent variable, let's perform a simple linear model to it.
You can download the dataset from <a href="https://www.dropbox.com/s/kquu5kzrqt9gtz7/Salary_Data.csv?dl=0">here</a>.
<img data-filename="1_Salary_Data.png" style="width: 195px;" src="/uploads/tutorials/2019/05/24_1_Salary_Data.png"> 
Let's plot the data in a graph.
<img src="https://lh5.googleusercontent.com/wW8uotB_FEcCRnVq9incsSaRaRc6S3tQ68COeqKxuUmG0xWlyJG1Sf1fPH2XDoLp8GT1XYQbVp50r09cSfkF641vfLD1GVKVsexim2RAIQIq6EAJ5XIX_qZ8a8T-bzyNYIVb4Usv" width="624" height="359" alt="wW8uotB_FEcCRnVq9incsSaRaRc6S3tQ68COeqKxuUmG0xWlyJG1Sf1fPH2XDoLp8GT1XYQbVp50r09cSfkF641vfLD1GVKVsexim2RAIQIq6EAJ5XIX_qZ8a8T-bzyNYIVb4Usv">
Look at the plot. The data is linear, independent, and equally distributed. So, it meets the assumptions of simple linear regression.
Now let's build a simple linear regression model with this dataset. You will get the full code in<a href="https://colab.research.google.com/drive/1r9oy5LUtgu1xtab9zuOUpXgGAnoI26k8?usp=sharing" target="_blank"> Google Colab</a>.&nbsp;
The first step will be preprocessing the dataset. As this model deals with just two variables, we can take the Experience column as the independent variable in the feature matrix X, and the Salary column as a dependent variable in the dependent variable vector y. <pre>#Simple Linear Regression
# Importing the essential libraries
import numpy as np 
import matplotlib.pyplot as plt 
import pandas as pd 
# Importing the dataset 
dataset = pd.read_csv('Salary_Data.csv') 
X = dataset.iloc[:, 0:1].values
y = dataset.iloc[:, 1].values</pre>Now, we will split the dataset between training and test sets. The training set will contain two-third of the data and the test set will have one-third of the data. You can try taking the arbitrary size for training and test sets. But keep in mind that the size of your datasets will make the model predict different outcomes. So, try to split the dataset in a way that helps the model to predict the best outcome.<pre># Splitting the dataset into the Training set and Test set 
from sklearn.model_selection import train_test_split 
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 1/3, random_state = 0)
</pre>Note: Here, random_state = 0 is used to ensure that when you run this code, the output will be the same as us. You could run your code perfectly without this parameter. Though the training data set and test data set may not look exactly like ours, still it will be fine.
 
After preprocessing the data, now we will build our simple linear regression model. To fit the model to our training set, we just need to use the linear regression class from the Scikit-Learn&nbsp;module. The code in Python is as follows:<pre># Fitting Simple Linear Regression to the Training set 
from sklearn.linear_model import LinearRegression 
regressor = LinearRegression() 
regressor.fit(X_train, y_train)
</pre>Now we have come to the final part. Our model is ready and we can predict the outcome! The code for this is as follows:<pre># Predicting the Test set results 
y_pred = regressor.predict(X_test)
</pre><h4> </h4><h4>Visualize Simple Linear Regression in Python</h4>We have come to the fun part. Now we will visualize the results in python. There are two different results. We will plot both in python.
To visualize the training set results:<pre># Visualising the Training set results 
plt.scatter(X_train, y_train, color = 'red') 
plt.plot(X_train, regressor.predict(X_train), color = 'blue') 
plt.title('Salary vs Experience (Training set)') 
plt.xlabel('Years of Experience') 
plt.ylabel('Salary') 
plt.show()
</pre><img src="/uploads/tutorials/2019/05/23_1_Simple_Linear_Regression.png" alt="23_1_Simple_Linear_Regression"> 
Here the graph represents the linear regression line(the blue straight line) for the training set data. The algorithm tries to find the best fit line for our dataset. So this line is the best fit line the algorithm could find for our data.
Now it is time to see how our model predicts on the test data:<pre># Visualising the Test set results 
plt.scatter(X_test, y_test, color = 'red') 
plt.plot(X_train, regressor.predict(X_train), color = 'blue') 
plt.title('Salary vs Experience (Test set)') 
plt.xlabel('Years of Experience') 
plt.ylabel('Salary') 
plt.show()
</pre><img src="/uploads/tutorials/2019/05/23_2_Simple_Linear_Regression.png" alt="23_2_Simple_Linear_Regression"> 
The above graph shows the predictions made by our simple linear regression model. The red dots are the test data and the blue line represents the predictions made by our model. If you look at the graph, our model made some close predictions for our test data(the dots on the line). Though the prediction is not accurate for some values(the dots far from the line), still it is a good simple linear regression model.
This is the simplest of all the regression models. In the following articles, we will see other complex regression models.
<h4>How to Improve a Simple Linear Regression Model?</h4>
The performance of our model is not that good. The regression line could not fit all the data points well. Therefore, we need improvements. There are many ways we can increase the accuracy of a simple linear regression model. Try the followings-<ul><li>Normalize the Data The data should&nbsp;be made normalized to get a more perfect model. There are normalizer functions you can apply to do so.</li><li>Remove Outliers If the dataset contains outliers i.e. values outside the normal distribution, the accuracy will not be improved. Remove the outliers to get better accuracy.</li><li>Check Collinearity If the data is correlated somehow, as I said earlier, the linear regression model will not perform well. Try to check and remove collinearity and then apply the model.</li></ul><h4>Final Thoughts</h4>In this article, I tried to explain everything you need to learn about linear regression. Started with what linear regression is and then show you the way how it works. Finally, we implemented a linear regression model in Python. Simple linear regression is the simplest implementation of regression models. It does not perform well for many types of data i.e. data with more than two variables. So, you can not always use it. Instead, you need to use other regression models.&nbsp;Hope this article helped you to understand simple linear regression well.&nbsp;Happy Machine Learning!

Learn Simple Linear Regression in the Hard Way(with Python Code)

<img data-filename="multiple_linear_regression_1.jpg" style="width: 1046px;" src="/uploads/tutorials/2020/08/10_multiple_linear_regression_1.jpg"> In this tutorial, we are going to understand the Multiple Linear Regression algorithm and implement the algorithm with Python.<h5>Tutorial Overview</h5><ul><li>What is Multiple Linear Regression?</li><li>Implement Multiple Linear Regression in Python</li><li>Improve Multiple Linear Regression model</li><li>Implement Backward Elimination in Python</li></ul><h4>What is Multiple Linear Regression?</h4>Multiple Linear Regression is closely related to a <a href="http://www.aionlinecourse.com/tutorial/machine-learning/simple-linear-regression">simple linear regression</a> model&nbsp;with the difference in the number of independent variables. Whereas the simple linear regression model predicts the value of a dependent variable based on the value of a single independent variable, in Multiple Linear Regression, the value of a dependent variable is predicted based on more than one independent variable. <h6>The Formula for Multiple Linear Regression</h6>The concept of multiple linear regression can be understood by the following formula- y = b0+b1*x1+b2*x2+..........+bn*xn
In the equation, y is the single dependent variable value of which depends on more than one independent variable (i.e. x1,x2,...,xn).
For example, you can predict the performance of students in an exam based on their revision time, class attendance, previous results, test anxiety, and gender. Here the dependent variable(Exam performance) can be calculated by using more than one independent variable. So, this the kind of task where you can use a Multiple Linear Regression model.
<h4>Implement Multiple Linear Regression in Python</h4>
Now, let's do it together. We have a dataset(Startups.csv) that contains the Profits earned by 50 startups and their several expenditure values. Les have a glimpse of some of the values of that dataset-&nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp;<img src="/uploads/tutorials/2019/08/18_2_Multiple_Linear_Regression.png" alt="18_2_Multiple_Linear_Regression">Note: this is not the whole dataset. You can download the dataset from <a href="https://www.dropbox.com/s/z2ue4a1ogefcuo3/50_Startups.csv?dl=0">here</a>.
From this dataset, we are required to build a model that would predict the Profits earned by a startup and their various expenditures like R &amp; D Spend, Administration Spend, and Marketing Spend. Clearly, we can understand that it is a multiple linear regression problem, as the independent variables are more than one.
Let's take Profit as a dependent variable and put it in the equation as y and put other attributes as the independent variables-
Profit = b0 + b1*(R &amp; D Spend) + b2*(Administration) + b3*(Marketing Spend)
From this equation, hope you can understand the regression process a bit clearer.
Now, let's jump to build the model, first the data preprocessing step. Here we will take Profit as in the dependent variable vector y, and other independent variables in feature matrix X. You will get the full code in<a href="https://colab.research.google.com/drive/1IvasQIAualkMMToZUpOJlXQPcWz30REN?usp=sharing" target="_blank"> Google Colab</a>.<pre># Importing the essential libraries
import numpy as np 
import matplotlib.pyplot as plt 
import pandas as pd 

#Importing the dataset 
dataset = pd.read_csv('50_Startups.csv') 
X = dataset.iloc[:, [0,1,2,3]].values 
y = dataset.iloc[:, 4].values
</pre>The dataset contains one categorical variable. So we need to encode or make dummy variables for that.<pre># Encoding categorical data
from sklearn.preprocessing import LabelEncoder, OneHotEncoder
labelencoder = LabelEncoder()
X[:, 3] = labelencoder.fit_transform(X[:, 3])
onehotencoder = OneHotEncoder()
X = onehotencoder.fit_transform(X).toarray()
</pre><h5>Solving the Dummy Variable Trap</h5>
&nbsp;The above code will make two dummy variables(as the categorical variable has two variations). And obviously, our linear equation will use both dummy variables. But this will make a problem. Here both dummy variables are correlated to some extent(that means one's value can be predicted by the other) &nbsp;which causes multicollinearity, a phenomenon where an independent variable can be predicted from one or more than one independent variable. When multicollinearity exists, the model cannot distinguish the variables properly, therefore predicts improper outcomes. This problem is identified as the Dummy Variable Trap.
To solve this problem, you should always take all dummy variables except one from the dummy variable set.<pre>#Avoiding the Dummy Variable Trap 
X = X[:, 1:]
</pre>Now split the dataset into a training set and test set<pre>#Splitting the dataset into the Training set and Test set
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, train_size = 0.8, test_size = 0.2, random_state = 0)
</pre>Its time to fit Multiple Linear Regression to the training set.<pre># Fitting Multiple Linear Regression to the Training set 
from sklearn.linear_model import LinearRegression 
regressor = LinearRegression() 
regressor.fit(X_train, y_train)
</pre>Let's evaluate our model how it predicts the outcome according to the test data.&nbsp;<pre>#Predicting the Test set result 
y_pred = regressor.predict(X_test)
</pre>Now, check how our model performed. For this, we will use the Mean Squared Error(MSE) metric from the Sciki-Learn library.<pre>from sklearn.metrics import mean_squared_error 
print("The Mean Squared Error is- {}".format(mean_squared_error(y_test, y_pred))) </pre><pre>The Mean Squared Error is- 83502864.03257468
</pre>The mean absolute error says our model has performed really bad on the test set. But we can improve the quality of the prediction by building a Multiple Linear Regression model with methods such as Backward Elimination, Forward Selection, etc. which we are going to discuss in the next chapter.
<h4>Improve Multiple Linear Regression Model</h4>
There are several ways to build a multiple linear regression model. They are-
<ul><li>All In In this method, all the independent variables are included in the model. The above model is built using this method. This is the simplest one but has serious drawbacks such as allowing colinear or redundant features in the model. In most cases, the model produces bad predictions.</li>
 <li>Backward Elimination It is a feature selection technique where all the insignificant features are eliminated. The final model will be built using the most important features or independent variables that have the most impact on the outcome.</li>
 <li>Forward Selection Opposite to the backward elimination method, this method starts with an empty model and adds independent variables one by one. In every forward step, the method adds the one variable which has the most impact on the outcome.</li>
 <li>Bidirectional Elimination This is a combination of the above two methods. In each step, the method checks if variables can be included or excluded to improve the outcome.</li>
</ul>In the tutorial, We are going to apply the backward elimination technique to improve our model. The steps involved in this technique are as follows-
Step 1: Select a statistical parameter e.g. p-value and set a significance level( e.g. p=0.05). A feature will be eliminated if it crosses this significance level.
Step 2: Fit the model with all the predictors
Step 3: Check the predictor with the highest p-value, if p&gt;0.05 go to step 4. If there is no such variable, your model is ready
Step 4: Remove the predictor
Step 5: Fit the model without this predictor.&nbsp;
Step 6: Repeat the 3rd, 4th, and 5th steps until you remove all the predictors above the significance level.
<h4>Implementing Backward Elimination in Python</h4>
Now, we will implement the backward elimination with our dataset to get an improved model than the previous one. For this task, we need to use the statsmodels api.
In our independent variable matrix, there is no column for constants. First of all, we need to append a constant column filled with 1's to the original matrix. Then we will make a list of all the features to build the initial model.<pre>import statsmodels.formula.api as sm 
X = np.append(arr=np.ones((50,1)).astype(int), values=X, axis=1) 
X_pred = X[:, [0, 1, 2, 3, 4, 5]]
</pre>In the second step, we will fit the list of predictors with a regressor model.<pre>Ols_regressor = sm.OLS(endog=y, exog=X_pred).fit()
</pre>Let's check statistics<pre>Ols_regressor.summary()
</pre><img src="/uploads/tutorials/2020/08/08_multiple_linear_regression.png" alt="08_multiple_linear_regression">
If you look at the p-value column, you can see, the third variable(Administration spend) has the highest p-value. So, in the next step, we are going to remove it and fit the model again with the rest variables.<pre>X_pred = X[:, [0, 1, 2, 4, 5]] 
Ols_regressor = sm.OLS(endog=y, exog=X_pred).fit() 
Ols_regressor.summary()
</pre>Again check the p-value
<img src="/uploads/tutorials/2020/08/08_multiple_linear_regression_3.png" alt="08_multiple_linear_regression_3">
The 3 rd variable(marketing spend) has a higher p-value than the significance level. We will remove this variable and fit the model again.
After repeating the above steps twice more, we have come to the final step<pre>X_pred = X[:, [0, 4, 5]] 
Ols_regressor = sm.OLS(endog=y, exog=X_pred).fit() 
Ols_regressor.summary()
</pre><img src="/uploads/tutorials/2020/08/08_multiple_linear_regression_5.png" alt="08_multiple_linear_regression_5">
Now, we can see all the variables have p-values less than the significance level. With these variables, we will build the prediction model.
First, divide the new matrix into training and test sets
<pre>#Splitting the dataset into the Training set and Test set
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X_pred, y, train_size = 0.8, test_size = 0.2, random_state = 0)</pre>
Again fit the multiple linear regression model with training set<pre># Fitting Multiple Linear Regression to the Training set 
from sklearn.linear_model import LinearRegression 
regressor = LinearRegression() 
regressor.fit(X_train, y_train)
</pre>Now, predict the value<pre>#Predicting the Test set result 
y_pred = regressor.predict(X_test)
</pre>Let's measure the accuracy to see whether we could improve the model<pre>from sklearn.metrics import mean_squared_error 
print("The Mean Squared Error is- {}".format(mean_squared_error(y_test, y_pred))) </pre><pre>The Mean Squared Error is- 1846130824.0073693
</pre>Wow! We made it! The mean absolute error has come down to 18%. So, the backward elimination method is very much helpful to build better multiple linear regression models.
<h4>Final Words</h4>
In this tutorial, I have tried to explain all the important aspects of multiple linear regression. The key takeaways of the tutorials are-
<ul><li>What is multiple linear regression</li>
 <li>Implementing multiple linear regression in Python</li>
 <li>Understanding different methods to improve the performance of a multiple linear regression model</li>
 <li>Implementing the backward elimination method</li>
</ul>Hope this tutorial helped you to understand all the concepts. If you have any questions or suggestions about the tutorial, please let me know in the comments.
Happy Machine Learning!

Multiple Linear Regression in Python (The Ultimate Guide)

<img src="/uploads/tutorials/2020/08/10_polynomial_regression_1.jpg" alt="10_polynomial_regression_1">
If you have worked with linear regression models such as <a href="http://www.aionlinecourse.com/tutorial/machine-learning/simple-linear-regression">simple linear regression</a> or <a href="http://www.aionlinecourse.com/tutorial/machine-learning/multiple-linear-regression">multiple linear regression</a>, you might have observed some drawbacks of those models. It is not like that the models are bad, rather it is due to the underlying property of your data. You see, data can take different shapes. And you need to use the right kind of algorithm to make the best predictive model out of your data.
In this tutorial, we are going to understand a different type of regression algorithm, the Polynomial Regression. After discussing the concepts, we will build a predictive model with the algorithm in Python. Let's dive into that!
<h4>What is Polynomial Regression?</h4>
Polynomial regression is a form of regression analysis in which the relationship between the independent variable x and dependent variable y is modeled as an nth degree polynomial of x. That is, if your dataset holds the characteristic of being curved when plotted in the graph, then you should go with a polynomial regression model instead of <a href="http://www.aionlinecourse.com/tutorial/machine-learning/simple-linear-regression">Simple</a>&nbsp;or <a href="http://www.aionlinecourse.com/tutorial/machine-learning/multiple-linear-regression">Multiple Linear regression</a>&nbsp;models.
The equation for Polynomial Regression looks very similar to that of Multiple Linear Regression.y=b0+b1*x1+b2*(x1)2+....+bn*(x1)n
The main difference is that in Multiple Linear Regression, there are several variables of the same degree but here the single variable has different powers.&nbsp;
<h4>Why Polynomial Regression?</h4>
Let's say you have a dataset and fit both Simple and Polynomial Regression to that data.
<img src="/uploads/tutorials/2019/05/24_1_linear.gif" alt="24_1_linear">
&nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; Plotted with a linear regression model
&nbsp;
Here you can see the data has a tendency to grow in a non-linear fashion. Hence a simple linear model could not find the most optimal line that can fit the data well and has a very poor accuracy level.
&nbsp;&nbsp;<img src="/uploads/tutorials/2019/05/23_2_polynomial.gif" alt="23_2_polynomial">
&nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp;Plotted with a polynomial regression model
Now if you look at the polynomial regression, you will clearly see the difference. The Polynomial model has fitted the dataset well with a higher accuracy rate than that of a simple linear model.
There are many cases where you will find great uses of polynomial regression. For example, if you want to discover how diseases spread, how a pandemic or epidemic spread over a continent, and so on. It completely depends on your data. And based on the non-linear characteristics of your data, you should use polynomial regression.
<h4>Implementing Polynomial Regression in Python</h4>
Now we will jump into a dataset and implement the above idea.
Suppose we have a dataset(Salary_data.csv) that contains the salaries of employees of different positions based on their Level. Let's have a look at the dataset.
<img src="/uploads/tutorials/2019/05/24_1_Position_Salary_Data_Table.png" alt="24_1_Position_Salary_Data_Table">
You can download the dataset from <a href="https://www.dropbox.com/s/ecwhriu55lx0xd6/Position_Salaries.csv?dl=0">here</a>.
If we plot the above data in a graph, it would look like this-
<img src="https://lh5.googleusercontent.com/4TGwABA2BlyYmv767MOB22CHLv5hLZ_AqWs1Ha712qL6t9ELF8wYcgOm7ZBxsj0j2Hq0om2wDyCvj3UHUJi55lISebn4luF7yi8kiRbHp2_DW0ueet10gjngGHQ0KZFJdh-1MjIt" width="624" height="371" alt="4TGwABA2BlyYmv767MOB22CHLv5hLZ_AqWs1Ha712qL6t9ELF8wYcgOm7ZBxsj0j2Hq0om2wDyCvj3UHUJi55lISebn4luF7yi8kiRbHp2_DW0ueet10gjngGHQ0KZFJdh-1MjIt">
Here, you can observe that our data has a tendency of growing non-linearly. So we are required to use a Polynomial Regression for this case.
The dataset contains just three columns. We will take the second column, Level as our independent variable in the feature matrix, X and the Salary column as the dependent variable in the dependent variable vector, y.
We start by preprocessing the data. You will get the full code in <a href="https://colab.research.google.com/drive/1unD0W0MxrDZRvSznTXxCn7I1L8jzjLBk?usp=sharing" target="_blank">Google Colab</a>. For this use the following codes-<pre># Polynomial Regression 
# Importing the Essential Libraries 
import numpy as np 
import matplotlib.pyplot as plt 
import pandas as pd 

# Importing the dataset 
dataset = pd.read_csv('Position_Salaries.csv') 
X = dataset.iloc[:, 1:2].values 
y = dataset.iloc[:, 2].values
</pre>We skip the splitting part as the dataset contains only 10 values. So let's fit polynomial regression to our whole dataset and for this, you should write the following code-<pre># Fitting Polynomial Regression to the dataset 
from sklearn.preprocessing import PolynomialFeatures 
from sklearn.linear_model import LinearRegression
poly_reg = PolynomialFeatures(degree = 4) 
X_poly = poly_reg.fit_transform(X) 
poly_reg.fit(X_poly, y) 
lin_reg_2 = LinearRegression() 
lin_reg_2.fit(X_poly, y)
</pre>Note: Here, I used degree = 4, you should try with different values for this parameter and watch how your model works. For this dataset, a value of degree 4 just works fine!
Well, we have fitted our model to the dataset. Now, it's time to plot and see how it works.<pre># Visualising the Polynomial Regression results 
X_grid = np.arange(min(X), max(X), 0.1) 
X_grid = X_grid.reshape((len(X_grid), 1)) 
plt.scatter(X, y, color = 'red') 
plt.plot(X_grid, lin_reg_2.predict(poly_reg.fit_transform(X_grid)), color = 'blue') 
plt.title('Truth or Bluff (Polynomial Regression)') 
plt.xlabel('Position level') 
plt.ylabel('Salary') 
plt.show()
</pre>The plot should look like this-
<img src="/uploads/tutorials/2019/05/23_3_Polynomial_Regression.png" alt="23_3_Polynomial_Regression">
With a 4-degree polynomial regression, we obtained a model that has closely predicted the Salary values. If we used a simple linear regression instead, we could not obtain this level of accuracy.
So now we can use our model to learn how it predicts for an unknown value.# Predicting an unknown value with Polynomial Regression model y_pred = lin_reg_2.predict(poly_reg.fit_transform([[6.5]]))
For a level value of 6.5, it predicts: 158862
We put the same dataset in a simple linear regression model. And for the same level value of 6.5, it gave us the outcome: 330378.78!
If you compare both the value with the first SALARY vs LEVEL graph, you can understand that our polynomial model has predicted a way better than that of a simple linear regression model.
<h5>How to Choose the Correct Degree of Polynomial for the Regression Model?&nbsp;</h5>
There is no "exact" way to choose the right value for the degree of a polynomial regression model. You can start with an initial value then continuously increase(or decrease) the values and check whether the curve fits your model more perfectly than the past one.
This process usually is not a good solution because it is hard to make this working every time i.e. think about a million-degree polynomial. This process will be time-consuming and complex which will not worth the effort. Because of the issue with overfitting.
When you are optimizing the polynomial equation to perfectly describe your data, you are making the model prone to overfitting. If you use this predictive model on unseen data, the performance will fall down in contrast to the training period. And this is not desirable for your model.
<a href="https://www.aionlinecourse.com/tutorial/machine-learning/k-fold-cross-validation">Cross-validation</a> can be handy to solve this problem. You can check a set of polynomial values with cross-validation. Then take the value which provided the best performance on average. This will prevent your model to overfit during the training stage. Although we are fitting a nonlinear model to the data, it is still a linear model. This is because the regression function takes into account the parameters, not the covariates(the number of degrees)
<h5>Is Polynomial Regression Linear or Non-Linear?</h5>
Although we are fitting a nonlinear model to the data, it is still a linear model. This is because the regression function takes into account the parameters, not the covariates(the number of degrees).
You can make any transformation to the variables, but still, the statistical estimation problem is linear.
For this, the polynomial variation is not considered as a different regression model. It is just a special case of multiple linear regression.&nbsp;
<h4>Final Words</h4>
In this tutorial, I have tried to discuss all the concepts of polynomial regression. The key take ways from the tutorial are-
<ul><li>What polynomial regression is and how it works</li>
 <li>Implementing polynomial regression in Python</li>
 <li>how to choose the best value for the degree of the polynomial</li>
</ul>Hope this tutorial has helped you to understand all the concepts. If you have any questions, please let me know in the comments.&nbsp;
Happy Machine Learning!

Polynomial Regression in Two Minutes (with Python Code)

<img style="width: 750px;" data-filename="svr_10.jpg" src="/uploads/tutorials/2020/07/22_svr_10.jpg"> Probably you haven't heard much about Support Vector Regression aka SVR. I don't know why this absolutely powerful regression algorithm has scarcity in uses. There are not good tutorials on this algorithm. I had to search a lot to understand the concepts while working with this algorithm for my project. Then I decided to prepare a good tutorial on this algorithm and here it is! In this article, we are going to understand Support Vector Regression. Then we will implement it using Python.
Support Vector Regression uses the idea of a Support Vector Machine aka SVM to do regression. Let's first understand SVM before diving into SVR
<h4>What is a Support Vector Machine?</h4>
Support Vector Machine is a discriminative algorithm that tries to find the optimal hyperplane that distinctly classifies the data points in N-dimensional space(N - the number of features). In a two-dimensional space, a hyperplane is a line that optimally divides the data points into two different classes. In a higher-dimensional space, the hyperplane would have a different shape rather than a line.
Here how it works. Let's assume we have data points distributed in a two-dimensional space like the following-
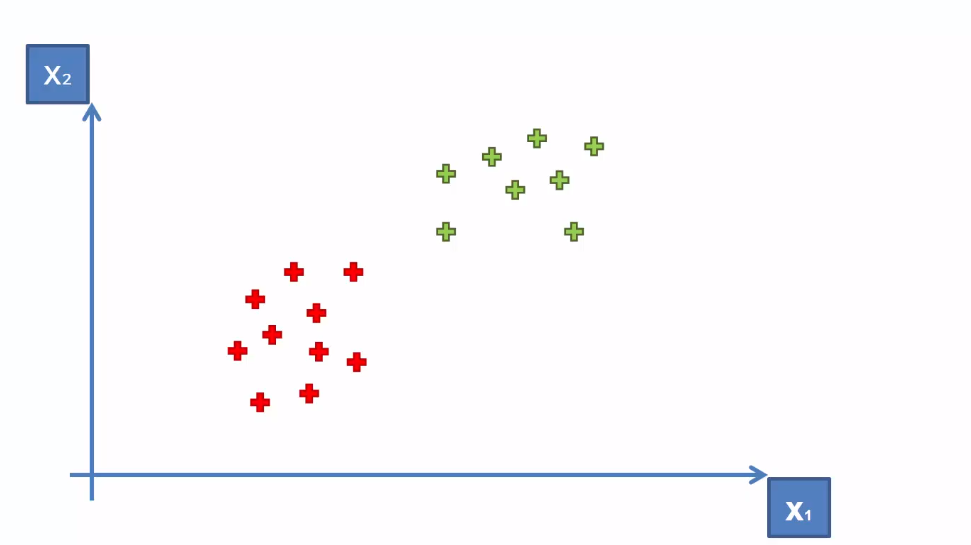
<img src="/uploads/tutorials/2020/07/22_11_SVM_1.png" alt="22_11_SVM_1">
SVM will try to find an optimal hyperplane. Here optimal refers to the line that can most equally divide the data. In other words, the line which will separate the two classes in a way that each class possibly contains the highest number of data points of its kind. After applying SVM to this data, the figure will look like the following-
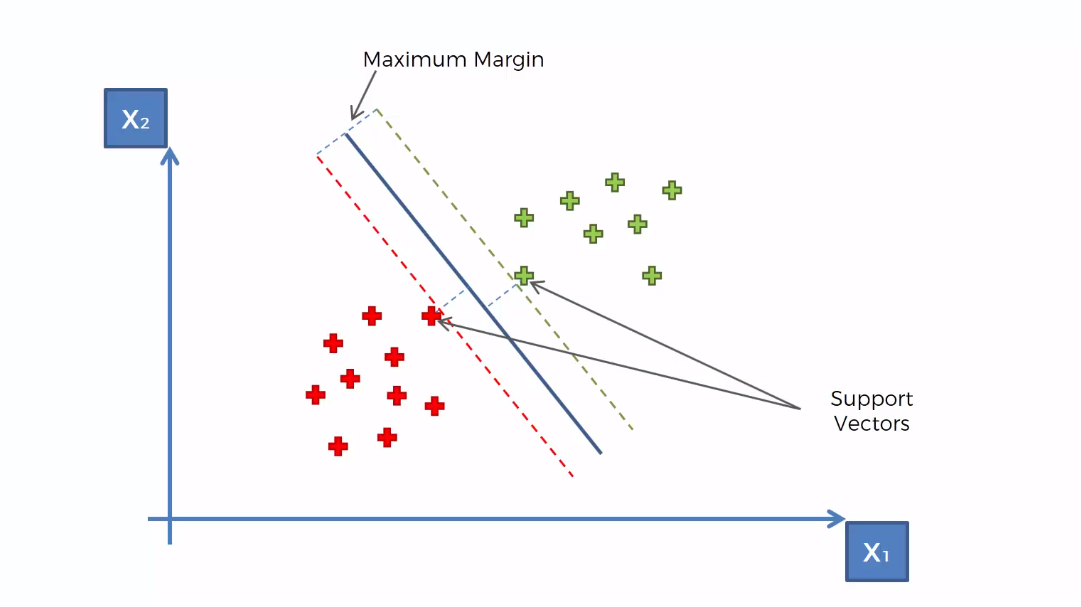
<img src="/uploads/tutorials/2020/07/22_11_SVM_3.png" alt="22_11_SVM_3">
In search of an optimal hyperplane, the SVM tries to find boundary data points or support vectors. The support vectors are chosen in such a way that the hyperplane will be at a possible maximum distance from both support vectors.
<h5>You may ask what is a support vector in a support vector machine?</h5>
Support vectors are those two data points supporting the decision boundary(the data points which have the maximum margin from the hyperplane). An SVM always tries to those two data points from different classes that are the closest to each other. These support vectors are the keys to draw an optimal hyperplane by SVM.&nbsp; In SVM, the set of input and output data are treated as vectors. This is because when the data is a higher-dimensional space(more than two dimensions), the classes cannot be represented as single data points, so they must be represented as vectors. And that's how it's got the name "Support Vector Machine".
I think you got the basic idea of SVM. Now, we can proceed to SVR-
<h4>Support Vector Regression Intuition</h4>
Support Vector Regression(SVR) is quite different than other Regression models. It uses the Support Vector Machine(SVM, a classification algorithm) algorithm to predict a continuous variable. While other linear regression models try to minimize the error between the predicted and the actual value, Support Vector Regression tries to fit the best line within a predefined or threshold error value. What SVR does in this sense, tries to classify all the prediction lines in two types, ones that pass through the error boundary( space separated by two parallel lines) and ones that don&rsquo;t. Those lines which do not pass the error boundary are not considered as the difference between the predicted value and the actual value has exceeded the error threshold, &#120750;(epsilon). The lines that pass, are considered for a potential support vector to predict the value of an unknown. The following illustration will help you to grab this concept.
.<img src="https://lh5.googleusercontent.com/xORUlTpVI2lLZ9VaRC9iyhVj0naiwROy9zDhaiNAwWzHPbpVLynDoTwLHAvKtkmCto3VVSrpvB1vuxkSgX92_qUO1_kpESSw36OTCfSx2KgYzuRKTSpD8muTXIFNw-Hr0gHw4zN2" width="624" height="333" alt="xORUlTpVI2lLZ9VaRC9iyhVj0naiwROy9zDhaiNAwWzHPbpVLynDoTwLHAvKtkmCto3VVSrpvB1vuxkSgX92_qUO1_kpESSw36OTCfSx2KgYzuRKTSpD8muTXIFNw-Hr0gHw4zN2">
Before analyzing the above illustration, first, understand some crucial definitions-
<ul><li>Kernel&nbsp;is a function that is used to map lower-dimensional data points into higher dimensional data points. As SVR performs linear regression in a higher dimension, this function is crucial. There are many types of kernels such as Polynomial Kernel, Gaussian Kernel, Sigmoid Kernel, etc.</li>
</ul><ul><li>Hyper Plane In Support Vector Machine, a hyperplane is a line used to separate two data classes in a higher dimension than the actual dimension. In SVR, a hyperplane is a line that is used to predict continuous value.</li>
</ul><ul><li>Boundary Line Two parallel lines drawn to the two sides of Support Vector with the error threshold value, &#120750;(epsilon) are known as the boundary line. These lines create a margin between the data points.</li>
</ul>From the above illustration, you clearly can understand the concept. The boundary is trying to fit as many instances as possible without violating the margin. The width of the boundary is controlled by the error threshold &#120750;(epsilon). In classification, the support vector X is used to define the hyperplane that separated the two different classes. Here, these vectors are used to perform linear regression. 
<h4>How Does Support Vector Regression Work?</h4>
<img src="/uploads/tutorials/2020/01/16_SVR_5.png" alt="16_SVR_5">
Let's do these steps one by one
First, choose a kernel, let's take the Gaussian kernel.
Now we come to the Correlation Matrix
&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;<img src="https://lh5.googleusercontent.com/u8v_AjKhvyH8JGFpLM3qeaIKM_Nz73MByrv-ua_tI_C2W3oFVerXxDunourX3_geOKOy5DmemWaJr7hTZ84flTcLfVq3GrR94mQBgjw3yrBCaObSj5iHOOTBH33jNuYBdXv9OAM7" width="339" height="145" alt="u8v_AjKhvyH8JGFpLM3qeaIKM_Nz73MByrv-ua_tI_C2W3oFVerXxDunourX3_geOKOy5DmemWaJr7hTZ84flTcLfVq3GrR94mQBgjw3yrBCaObSj5iHOOTBH33jNuYBdXv9OAM7">
In the equation above, we are evaluating our kernel for all pairs of points in our training set and adding the regularizer resulting in the matrix.
<img src="/uploads/tutorials/2020/01/16_SVR_6.png" alt="16_SVR_6">
Then we estimate the elements of the coefficient matrix by the following:
&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;
&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;<img src="https://lh4.googleusercontent.com/YFPI5Lighu_pDuBIwYKAafkIwY3hVu9jyMPrqdmZtpvOgZqTRxYvPTQtfe7iezAgUORuHCQU-ginmhRcIL6ywkk5urxr25-jPHNvqySwoljmP_C5ma36fKNBGZfSseElb1qf1Lxh" width="279" height="86" alt="YFPI5Lighu_pDuBIwYKAafkIwY3hVu9jyMPrqdmZtpvOgZqTRxYvPTQtfe7iezAgUORuHCQU-ginmhRcIL6ywkk5urxr25-jPHNvqySwoljmP_C5ma36fKNBGZfSseElb1qf1Lxh">
That's all! These crucial steps are everything you need to understand and perform support vector regression. 
<h4>Support Vector Regression in Python</h4>
Pythons' Scikit-Learn module provides all the functions to implement SVR. All we need to take a data set and prepare it to fit an SVR model.
For this tutorial, we choose a data set that provides the salary of employees along with their position and level. Let's have a look at the data-
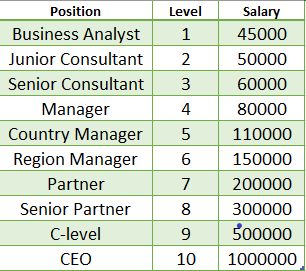
&nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp;<img src="/uploads/tutorials/2020/01/16_SVR_7.png" alt="16_SVR_7">
You can download the dataset from <a href="https://www.dropbox.com/s/ecwhriu55lx0xd6/Position_Salaries.csv?dl=0">here.</a>
This dataset contains the position and level of some employees and according to this level, the salary is calculated. Let's check the graph of this dataset
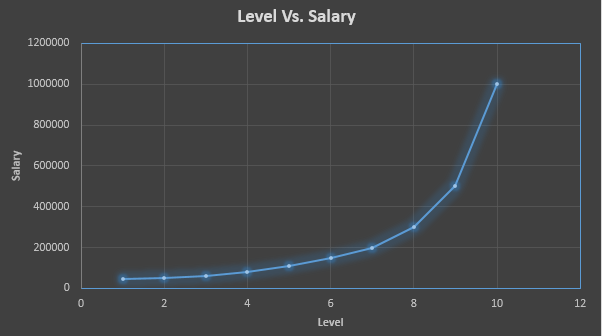
<img src="/uploads/tutorials/2020/01/16_SVR_8.png" alt="16_SVR_8">
The graph shows that the data is non-linear. Now, what if we want to learn the salary for a level of 6.5. What would be that? To predict that, we will implement Support Vector Regression. You will get full code in <a href="https://colab.research.google.com/drive/1tA3brCULHeP3_DlUQMt55P2DTrWzSEAH?usp=sharing" target="_blank">Google Colab</a>.
First of all, include the essential libraries<pre># Importing the libraries 
import numpy as np 
import matplotlib.pyplot as plt 
import pandas as pd
</pre>Let's import the dataset and make the feature matrix and the dependent variable vector<pre># Importing the dataset 
dataset = pd.read_csv('Position_Salaries.csv') 
X = dataset.iloc[:, 1:2].values 
y = dataset.iloc[:, 2].values
</pre>Now, we need to feature scale the data<pre># Feature Scaling 
from sklearn.preprocessing import StandardScaler 
sc_X = StandardScaler() 
sc_y = StandardScaler() 
X = sc_X.fit_transform(X) 
y = sc_y.fit_transform(y.reshape(-1, 1))
</pre>Now, we need to feature scale the data<pre># Fitting SVR to the dataset 
from sklearn.svm import SVR 
regressor = SVR(kernel = 'rbf') 
regressor.fit(X, y)
</pre>Fit the SVR algorithm to the dataset Let's predict the result<pre># Predicting a new result 
y_pred = regressor.predict([[6.5]]) 
y_pred = sc_y.inverse_transform(y_pred)
</pre>Finally, we can now visualize what our model has done!<pre># Visualising the SVR results 
plt.scatter(X, y, color = 'red') 
plt.plot(X, regressor.predict(X), color = 'blue') 
plt.xlabel('Position level') 
plt.ylabel('Salary') 
plt.show()
</pre>Let's have a look at the graph
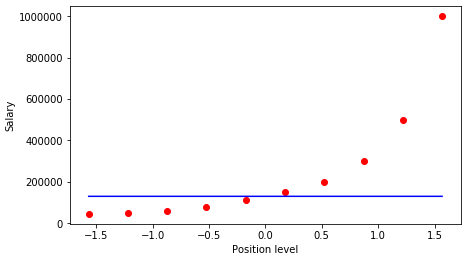
&nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp;<img src="/uploads/tutorials/2020/01/16_SVR_9.png" alt="16_SVR_9"> 
<h4>Multi-output Support Vector Regression in Python</h4>
In our example, we took a data set with a single output variable. What if you need to find multiple outputs? Suppose we add a new attribute named Job Satisfaction into our data set which will describe how much satisfaction the employees get in an inclusive range of one to ten. Now our model would have to predict two outputs. Can we do that with our existing model?
The answer is no. SVR is inherently suitable to work with a single output problem. But sometimes you need to work with data containing multiple outputs(like the above example). In Scikit-learn there is a class named MultiOutputRegressor which can be used as a base regressor that will take an SVR to perform a multi-output regression task. The trick here is to train&nbsp;a separate SVR for each output. If there is any correlation between the target outputs, it will not consider that correlation. Hence, some issues may come out when your output variables hold correlations among them. In that case, you should use decision tree-based regression algorithms. Decision trees inherently handle multiple outputs and may perform better than SVR.&nbsp;
Let's talk about some applications of support vector regression. Though SVR sounds like just a regression algorithm, it has great uses in many areas especially in time series forecasting for stock prices. 
<h4>Support Vector Regression for Time-series Forecasting</h4>
Recall the idea of SVR. Here, you give a set of input vectors and defined an output. The SVR then fits a model and tries to learn from those input vectors and finally predicts the response for a given new input vector. While working with time series data like stock prices, you need to determine which will be the "feature vector".&nbsp;This is because time series data is time-dependent i.e. there will be a lot of past values and you can not take everything as feature vectors. For example, you have a stock price data set that contains the prices of a single stock from the previous six months. Now, based on this data you want to forecast the future price of the stock.
Here, you have to transform the past data to build some feature vectors. There are many ways you can do this i.e. averaging the past one month's prices or the current price of the stock divided by the moving average. This will minimize the input vectors and make it easier for the SVR to fit them. SVR features are unordered x-y pairs, so you can not get a model that considers time order. If you want to maintain the time order, you can build separate SVRs i.e. one for the past 10 days, one for the past 1 month, etc. and then take the average of all the predictions and forecast the values.<h4>Advantages and Disadvantages of Support Vector Regression</h4>There are some key benefits to choose a support vector machine for regression tasks. There are some drawbacks as well. Let's talk about them-The key advantages are-<ul><li>SVM works really well with high-dimensional data. If your data is in higher dimensions, it is wise to use SVR.</li><li>For data with a clear margin of separations, SVM works relatively well.</li><li>When data has more features than the number of observations, SVM is one of the best algorithms to use.</li><li>As a discriminative model, it need not to memorize anything about data. Therefore, it is memory efficient.&nbsp;</li></ul>Some drawbacks are-<ul><li>It is a bad option when the data has no clear margin of separation i.e. the target class contains overlapping data points.</li><li>It does not work well with large data sets.</li><li>For being a discriminative model, it separates the data points below and above a hyperplane. So, you will not get any probabilistic explanation of the output.</li><li>It is hard to understand and interpret SVM as its underlying structure is quite complex.</li></ul><h4>Support Vector Machine Vs. Support Vector Regression</h4>We discussed at the beginning that supports vector regression uses the idea of a support vector machine, a discriminative classifier actually, to perform regression. In a sense of operative nature, they are different. SVM performs classification where SVR performs regression. That's the basic difference between an SVM and an SVR. Are there other differences?Well, yes. The differences lie in their optimization functions. 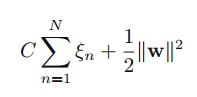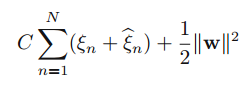The optimization function for an SVM is-<img style="width: 197px;" data-filename="svr_12.png" src="/uploads/tutorials/2020/07/23_svr_12.png">While SVR uses a slightly different optimization function-<img style="width: 250px;" data-filename="svr_11.png" src="/uploads/tutorials/2020/07/23_svr_11.png"> <h4>Final Thoughts</h4>In the tutorial, I tried to explain to you all the major aspects of support vector regression. The key takeaways of the tutorial are-<ul><li>Understanding what a Support Vector Machine is.</li><li>The Intuition behind Support Vector Regression and implementing it in Python.</li><li>The major uses of SVR and the advantages and disadvantages of using it.</li></ul>Hope you got a clear idea about the topic. If you have any questions in mind about the concepts, please let me know in the comments. Your feedback will help me to make it better.Happy Machine Learning!

Support Vector Regression Made Easy(with Python Code)

<img src="/uploads/tutorials/2020/08/10_decision_tree_regression.jpg" alt="10_decision_tree_regression">
In this tutorial, we are going to understand the decision tree regression and implement it in Python
<h4>What is a Decision Tree?</h4>
This Regression is based on the decision tree structure. A decision tree is a form of a tree or hierarchical structure that breaks down a dataset into smaller and smaller subsets. At the same time, an associated decision tree is incrementally developed. The tree contains decision nodes and leaf nodes. The decision nodes(e.g. Outlook) are those nodes that represent the value of the input variable(x). It has two or more than two branches(e.g. Sunny, Overcast, Rainy). The leaf nodes(e.g. Hours Played) contain the decision or the output variable(y). The decision node that corresponds to the best predictor becomes the topmost node and called the root node.
&nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; <img src="/uploads/tutorials/2019/05/28_1_Decision_tree_Regression.png" alt="28_1_Decision_tree_Regression">
Decision Trees are used for both Classification and Regression tasks. In this tutorial, we will focus on Regression trees.
Let's consider a scatter plot of a certain dataset.
&nbsp; &nbsp;
&nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp;&nbsp;<img src="/uploads/tutorials/2018/09/19_Decision_tree_3.png" alt="19_Decision_tree_3">
Here, we take a dataset that contains two independent variables X1, and X2 and we are predicting a third dependent variable y. You can not find it on the scatterplot as it has two dimensions. To visualize y, we need to add another dimension and after that, it would like the following:
&nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp;<img src="/uploads/tutorials/2018/09/19_Decision_tree_4.png" alt="19_Decision_tree_4">
<h4>How Does a Decision Tree Work for Regression?</h4>
Well, for this our decision tree would make some splits on the dataset based on information entropy( information entropy tells how much information there is in an event). This is basically dividing the points into some groups. The algorithm decides the optimal number of splits and splits the dataset accordingly. The figure will make it clear
&nbsp;
&nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp;<img src="/uploads/tutorials/2018/09/19_Decision_tree_5.png" alt="19_Decision_tree_5">
Here we can see the decision tree made four splits and divided the data points into five groups.
Now, this algorithm will take the average value of each group and based on that values it will build the decision tree for this dataset. The tree would look like the following:
&nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp;<img src="/uploads/tutorials/2019/05/28_2_Decision_Tree.png" alt="28_2_Decision_Tree">
The decision tree above shows that whenever a value of y falls in one of the leaves, it will return the value of that leaf as the prediction for that y value.
<h4>Implementing Decision Tree Regression in Python</h4>
Let's implement the above idea in Python. We will work on a dataset (Position_Salaries.csv) that contains the salaries of some employees according to their Position. Our task is to predict the salary of an employee according to an unknown level. So we will make a Regression model using Decision Tree for this task.
You can download the dataset from <a href="https://www.dropbox.com/s/ecwhriu55lx0xd6/Position_Salaries.csv?dl=0">here.</a>
First of all, we will import the essential libraries. You will get the full code in <a href="https://colab.research.google.com/drive/1hG-AbDtlrMsHQiQcUGykEbEzqP1T-AeV?usp=sharing" target="_blank">Google Code</a>.&nbsp;
<pre># Importing the Essential Libraries import numpy as np
import pandas as pd import matplotlib.pyplot as plt</pre>

Then, we import our dataset.
<pre># Importing the Dataset dataset = pd.read_csv("Position_Salaries.csv")</pre>

After executing this code, the dataset will be imported into our program. Let's have a look at that dataset:
&nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp;&nbsp;<img src="/uploads/tutorials/2018/09/19_Decision_tree_7.png" alt="19_Decision_tree_7">
Now, we need to determine the dependent and independent variables. Here we can see the Level is an independent variable while Salary is the dependent variable or target variable as we want to find out the salary of an employee according to his Level. So our feature matrix X will contain the Level column and the value of Salary is taken into the dependent variable vector, y.
<pre># Creating Feature Matrix and Dependent Variable Vector X = dataset.iloc[:, 1:2].values
y = dataset.iloc[:, 2].values</pre>
Now, we use DecisionTreeRegressor class from the Scikit-learn library and make an object of this class. Then we will fit the object to our dataset to make our model.
<pre># Fitting Decision Tree Regression to the dataset from sklearn.tree import DecisionTreeRegressor
regressor = DecisionTreeRegressor(random_state = 0) regressor.fit(X, y)</pre>

Well, our model is ready!&nbsp; Let's test our model to know how it predicts an unknown value.
<pre># Predicting a new result y_pred = regressor.predict([[6.5]])</pre>

We predict the result of &nbsp;6.5 level salary. After executing the code, we get an output of $150k. To learn how closely our model predicted the value, <h4>Visualizing Decision Tree Regression in Python</h4>lets visualize the training set.
<pre># Visulizing the Training Set X_grid = np.arange(min(X), max(X), 0.01) X_grid = X_grid.reshape((len(X_grid), 1)) plt.scatter(X, y, color = 'red')
plt.plot(X_grid, regressor.predict(X_grid), color = 'blue') plt.title('Decision Tree Regression') plt.xlabel('Position level') plt.ylabel('Salary')
plt.show()</pre>


&nbsp;The plot would look like this:
&nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp;&nbsp;<img src="/uploads/tutorials/2019/05/28_5_Decision_Tree_Regression.png" alt="28_5_Decision_Tree_Regression">
After executing the code, we can see a graph, where we plotting a prediction of &nbsp;10 salaries corresponding to 10 levels. It is a nonlinear and non-continuous regression model. This graph does not look like the other linear regression models. Because the decision tree regression takes the average value of each group and assigns this value for any variable that falls in that group. So the graph is not continuous rather it looks like a staircase.
From the graph, we see that the prediction for a 6.5 level is pretty close to the actual value(around $160k). So we can say it is a good regression model.
<h4>Advantages and Disadvantages of Decision Tree Regression</h4>
Decision tree for regression comes with some advantages and disadvantages, let's have a look at them-
<h5>Advantages</h5>
<ul><li>Less Data Preprocessing&nbsp;Unlike other machine learning algorithms, a decision tree does not require well-preprocessed data.&nbsp;</li>
 <li>No Normalization&nbsp;Decision tree does not require normalized data</li>
 <li>No Scaling&nbsp;You need not scale the data before feeding it to the decision tree model</li>
 <li>Not Affected by Missing Value&nbsp;Unlike K nearest Neighbor or other distance-based algorithms, a decision tree is not affected by missing values</li>
 <li>Easy and Intuitive&nbsp;A decision tree is intuitive and fairly easy to understand and explain the underlying properties</li>
</ul><h5>Disadvantages</h5>
<ul><li>Highly Sensitive&nbsp;A small change in data can cause high instability to a decision tree model</li>
 <li>Complex Calculation&nbsp;A decision tree uses more complex computation compared to other models</li>
 <li>High Training Time&nbsp;It takes higher time to train a decision tree model</li>
 <li>Costly&nbsp;Decision tree-based models require more space and time, so it is computationally expensive to use</li>
 <li>Weak&nbsp;A single tree can not learn much of the data, therefore, you won't get a good predictor using a single decision tree. You need to ensemble a higher number of decision trees e.g. random forest to get better prediction accuracy</li>
</ul><h4>Decision Tree Regression FAQs</h4>
Here I answered some of the frequently asked questions about decision tree regression
<h5>What is Entropy in a Decision Tree?</h5>
By definition, entropy is the measure of the total disorder in a system. A decision tree uses a top-down approach to build a model by continuously splitting the data into small portions. Before each split, It calculates the entropy to understand the information gain it would get from a split. Entropy is the main input to the information gain equation. The Decision tree model calculates the entropy for the parent node and the child node, and then it finds the information gain using these two measures. The formula for entropy is like the following-
<img src="/uploads/tutorials/2020/08/11_decision_tree_regressio_entropy.png" alt="11_decision_tree_regressio_entropy">
Here
<ul><li>E represents the measure of entropy</li>
 <li>Pi is the probability of a class or feature in each split</li>
</ul>This entropy is used in an information gain equation which is like the following-
<img src="/uploads/tutorials/2020/08/11_decision_tree_regressio_information_gain.png" alt="11_decision_tree_regressio_information_gain">
Here
<ul><li>IG represents the information gain</li>
 <li>E(Y) is the entropy measure of a parent node</li>
 <li>E(Y|X) is the measure of the child node</li>
</ul>The goal of a decision tree model is to decrease entropy and increase the information gain.
<h5>Which Node has Maximum Entropy in a Decision Tree?</h5>
It depends on the majority of features. When a node has all homogenous data i.e. all the data points are similar, the entropy will be the lowest. But when the node contains data points equally from each feature, in other words, there is no majority of a particular feature, then the node will experience the maximum entropy.
<h5>How to Find the Best Split in a Decision Tree?</h5>
The split is done by calculating the total value of information gain. Higher information gain is dependent on the lower entropy of a node. So, to find the best split, we need to decrease the entropy of a node. This will help to increase the information gain, resulting in the best split for the decision tree.
<h5>What is the Difference Between a Classification Tree and a Regression Tree?</h5>
&nbsp;Both classification and regression use the same decision tree structure. Hence, there are not many differences between regression and a classification tree. Some of the key differences are-
<ul><li>Regression tree uses continuous features whereas classification tree works with categorical features</li>
 <li>While splitting, a regression tree takes the mean of values from a group of data points. But classification tree takes the mode from a group of data points.</li>
 <li>A regression tree predicts the mean value of a class where a classification tree predicts the class which has the highest mode in a group</li>
</ul><h4>Final Words</h4>
In this tutorial, I tried to explain all the aspects of the decision tree for regression. The key take ways from the tutorial are
<ul><li>What a decision tree is and how it works for regression</li>
 <li>Implementing decision tree for regression using python</li>
 <li>Advantages and disadvantages of decision trees</li>
 <li>Some important questions about decision trees</li>
</ul>Hope this tutorial has helped you to understand all the concepts clearly. If you have any questions about the tutorial, let me know in the comments.&nbsp;
Happy Machine Learning!

Decision Tree Regression Made Easy (with Python Code)

<h4><img data-filename="random_forest.jpg" style="width: 768px;" src="/uploads/tutorials/2020/08/10_random_forest.jpg"></h4>In this tutorial, we will understand the decision tree regression algorithm and implement it in Python.<h4>What is a Random Forest?</h4>Random Forest is a supervised learning algorithm.&nbsp;The basic idea behind Random Forest is that it combines multiple decision trees to determine the final output. That is it builds multiple decision trees and merges their predictions together to get a more accurate and stable prediction.
<h4>How Does Random Forest Work?</h4>
.It uses the ensemble learning technique(Ensemble learning is using multiple algorithms at a time or a single algorithm multiple times to make a model more powerful) to build several decision trees at random data points. Then their predictions are averaged. Taking the average value of predictions made by several decision trees is usually better than that of a single decision tree. Look at the following illustration of two trees(though the number of trees is much more!) 
&nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp;<img src="/uploads/tutorials/2018/09/19_random_1.png" alt="19_random_1">
<h5>What is Random in Random Forest?</h5>Random forest uses 'randomness' in two cases-<ul><li>Random Sample Selection Random tree ensembles a set of decision trees. While training an individual decision tree, a random sample of training data is used. This method is called bootstrapping where many data sets are developed from the original data set by taking random samples. This way random forest could train more and more decision trees.</li><li>Random Variable Selection During each split, a random subset of features is examined. Then the set of variables that would provide the best split is chosen for the split. This random selection reduces the correlations among the trees and improves the predictive performance of the model.</li></ul><h5>The Steps Required to Perform Random Forest Regression</h5>
Step 1: Pick at random k data points from the training set.
Step 2: Build the decision Tree associated with this K data point.
Step 3: Choose the number Ntree of trees you want to build and repeat STEPS 1 &amp; 2.
Step 4: For a new data point, make each one of our Ntree trees predict the value of Y for the data point in question and assign the new data point the average across all of the predicted Y values. Now let's do these steps in Python.
<h4>Implementing Random Forest Regression in Python</h4>
In this tutorial, we will implement Random Forest Regression in Python. We will work on a dataset (Position_Salaries.csv) that contains the salaries of some employees according to their Position. Our task is to predict the salary of an employee at an unknown level. So we will make a Regression model using Random Forest technique for this task.
You can download the dataset from <a href="https://www.dropbox.com/s/ecwhriu55lx0xd6/Position_Salaries.csv?dl=0">here.</a>
First of all, we will import some essential libraries. You will get the code in <a href="https://colab.research.google.com/drive/1JhkfGT1LqS-YvyOZYUdyH5hSOvG-_Cwm?usp=sharing" target="_blank">Google Colab</a> also.
<pre># Importing the Essential Libraries 
import numpy as np 
import matplotlib.pyplot as plt import pandas as pd</pre>Then we will import the dataset.<pre style="font-size: 14px;"># Importing the Dataset 
dataset = pd.read_csv("Position_Salaries.csv")</pre>


Now our dataset has imported into our program. Let's check how it looks:
 
&nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp;<img src="/uploads/tutorials/2019/05/28_2_Random_Forest_Dataset.png" alt="28_2_Random_Forest_Dataset"> 
Now, we need to determine the dependent and independent variables. Here we can see the Level is an independent variable while Salary is the dependent variable or target variable as we want to find out the salary of an employee according to his Level. So our feature matrix X will contain the Level column and the value of Salary is taken into the dependent variable vector, y.
 <pre># Creating Feature Matrix and Dependent Variable Vector
X = dataset.iloc[:, 1:2].values 
y = dataset.iloc[:, 2].values
</pre>
Well, we have come to the main part of the Regression. To implement Random Forest Regression, we need RandomForestRegressor class from Scikit-Learn library.&nbsp;Check that we did not normalize or scale the data. Is not scaling necessary in random forest?The answer is no. Random forest is a tree-based algorithm that does not require convergence and numerical precision of data. Unlike other distance-based algorithms such as k-nearest neighbors, where scaling is required so that the priority is not given to specific features.If you still apply feature scaling to your data, the result will be the same as before. So, why bother? Just fit the model to the random forest regressor.<pre>from sklearn.ensemble import RandomForestRegressor
regressor = RandomForestRegressor(n_estimators = 10, random_state = 0)
regressor.fit(X, y)
</pre>
Note: Here, n_estimators is a parameter that sets the number of decision trees created for a random data point(the default value is 10, you can use a more number of trees). random_state = 0 is used so that your code provides the same output as us.
Our model is ready! Now, we will test our model for a new value of y.<pre># Predicting a New Value 
y_pred = regressor.predict([[6.5]])
</pre>Our model predicted a value of $167k. Let's compare this value with the actual value. For this, we will visualize our training set result.<pre># Visualizing the Training Set X_grid = np.arange(min(X), max(X), 0.01)
X_grid = X_grid.reshape((len(X_grid), 1))
plt.scatter(X, y, color = 'red')
plt.plot(X_grid, regressor.predict(X_grid), color = 'blue')
plt.title('Truth or Bluff (Random Forest Regression)')
plt.xlabel('Position level')
plt.ylabel('Salary')
plt.show()
</pre>&nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp;<img src="/uploads/tutorials/2019/05/28_4_Random_Forst_Regression.png" alt="28_4_Random_Forst_Regression">
After executing the code, we can see a graph, which is pretty similar to that of a <a href="http://www.aionlinecourse.com/tutorial/machine-learning/decision-tree-intuition">Decision Tree Regression</a>. The main difference is that the lines are more discontinuous from the Decision Tree regression. This is because Random Forest uses a number of decision trees to predict the value of a data point.&nbsp;
From the graph, we see that the prediction for a 6.5 level is pretty close to the actual value(around $160k).<h4 style='font-family: -apple-system, BlinkMacSystemFont, "Segoe UI", Roboto, Oxygen, Ubuntu, Cantarell, "Fira Sans", "Droid Sans", "Helvetica Neue", sans-serif; color: rgb(0, 0, 0);'>Improving the Accuracy of Random Forest Regression</h4>We have built a very simple model. There are many things that can be done to make a more improved model. Let's look at them-<ul><li>Add More Data&nbsp;For the sake of simplicity, we took a small data set. To make a more robust and well-performing model you should add more data. As the random forest model uses multiple decision trees, more data will increase the variance, eventually leading to a better predictive model.</li><li>Better Data Preprocessing&nbsp;Before feeding to the model, handle missing values properly. You should check if the data contain outliers. Outliers can seriously damage your model accuracy. Remove outliers to build a better-performing model.</li><li>Use Feature Selection Methods&nbsp;You should feed the model with the most appropriate features it requires to make a good model. For this, you can use some feature selection techniques to remove redundant and correlated features. Then feed the data to the random forest model.</li><li>Apply Cross-Validation&nbsp;Random forest resembles a set of individual trees and take their average predictions in the final model. Hence, there are some chances that data overlap (same data being used in many trees) which will lead to overfitting the model. You should use some sort of&nbsp;<a href="https://www.aionlinecourse.com/tutorial/machine-learning/k-fold-cross-validation" target="_blank">cross-validation technique</a>&nbsp;to make sure the model does not overfit.</li><li>Hyperparameter Tuning&nbsp;Random forest algorithm uses a number of hyperparameters. You need to carefully choose the best hyperparameters to make the best model. User grid search or random search methods to find the best hyperparameters to build the perfect model.</li></ul><h4>Decision Trees Vs. Random Forest</h4>Random Forest is a collection of Decision Trees, but there are some differences. If you input a training dataset with features and labels into a decision tree, it will formulate some set of rules, which will be used to make the predictions.Another difference is that decision trees might suffer from&nbsp;Overfitting. Random Forest prevents overfitting most of the time, by creating random subsets of the features and building smaller trees using these subsets. Afterward, it combines the subtrees. Note that this doesn't work every time and that it also makes the computation slower, depending on how many trees your random forest builds.Random Forest is a flexible, easy to use machine learning algorithm that produces, even without hyper-parameter tuning, a great result most of the time. It is also one of the most used algorithms because of its simplicity and the fact that it can be used for both classification and regression tasks. In this post, you are going to learn, how the random forest algorithm works and several other important things about it.<h4>Final Words</h4>In this tutorial, I have tried to explain all the aspects of random forest regression. The key takeaways of the tutorial are-<ul><li>What random is forest and how it works</li><li>Implementation in Python</li><li>Ways to improve the random forest model</li></ul>Hope this tutorial helped you to understand all the concepts. You have any questions about the concepts, please ask me in the comments.&nbsp;Happy Machine Learning!

Random Forest Regression in 4 Steps(with Python Code)

<img data-filename="evaluating regression models performance.jpg" style="width: 1046px;" src="/uploads/tutorials/2020/08/10_evaluating_regression_models_performance.jpg"> The performance of a regression model can be understood by knowing the error rate of the predictions made by the model. You can also measure the performance by knowing how well your regression line fit the dataset.
In this post, we will try to understand how to measure the performance of regression models.
A good regression model is one where the difference between the actual or observed values and predicted values for the selected model is small and unbiased for train, validation and test data sets.
To measure the performance of your regression model, &nbsp;some statistical metrics are used. Here we will discuss four of the most popular metrics. They are-
<ul><li>
 Mean Absolute Error(MAE)
 </li>
 <li>
 Root Mean Square &nbsp;Error(RMSE)
 </li>
 <li>
 Coefficient of determination or R2
 </li>
 <li>
 Adjusted R2</li></ul><h4>Mean Absolute Error(MAE)</h4>
This is the simplest of all the metrics. It is measured by taking the average of the absolute difference between actual values and the predictions.
&nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp;&nbsp;<img src="/uploads/tutorials/2019/05/29_1_Evaluating_Regression_Performance.jpg" alt="29_1_Evaluating_Regression_Performance" style="width: 100%;"> 
 
Suppose we have a model that predicted the salary of 4 employees which are $988, $1943, $1239, $2124 where the actual salaries were $1000, $1500, $2000. $2500 respectively.
If we take the absolute difference of the predictions and the actual values we get:
 <pre>| 1000 - 988 | = 12
| 1500 - 1943 | = 443
| 2000 - 1239 | = 761
| 2500 - 2124 | = 376 Now, MAE = (12 + 443 + 761 + 376) / 4
 = 398
</pre>
What does this MAE value mean? This value tells us that the model is predicting &nbsp;$398 more or less on average than the actual value.Note: The less the value of MAE the better the performance of your model.
<h4>Root Mean Square &nbsp;Error(RMSE)</h4>
The Root Mean Square Error is measured by taking the square root of the average of the squared difference between the prediction and the actual value. It represents the sample standard deviation of the differences between predicted values and observed values(also called residuals). It is calculated using the following formula:
&nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp;&nbsp;<img src="/uploads/tutorials/2019/05/29_2_RMSE.jpg" alt="29_2_RMSE">
If we take our previous example again, then we have-<pre>RMSE = sqrt((122 + 4432 + 7612 + 3762) / 4)
 ~478 
*sqrt = Sqare Root
</pre>
Here the RMSE value is greater than that of MAE. This is because RMSE takes the square of the differences between the predictions and the actual value, hence the value is greater the MAE value.
Both MAE and RMSE are in the same units as the dependent variable. As compared to MAE, RMSE will give higher weight to the errors and punish large errors in the model. RMSE is the default metric of many models as the loss function defined in terms of RMSE is smoothly differentiable and makes it easier to perform mathematical operations.RMSE is a better performance metric as it squares the errors before taking the averages. For that, large errors receive higher punishment. It performs particularly well when large errors are undesirable for your model's performance.
Note: When you have more samples then reconstructing the error distribution using RMSE is more reliable. But RMSE is highly sensitive to outlier values(an outlier is a data point that differs significantly from other observations). Hence, prior to using this metric, you must remove the outliers from your data set.
<h4>Coefficient of Determination or R^2</h4>
It measures how well the actual outcomes are replicated by the regression line. It helps you to understand how well the independent variable adjusted with the variance in your model. That means how good is your model for a dataset. The mathematical representation for R^2 is-
&nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp;<img src="/uploads/tutorials/2019/05/29_3_R2_equation.gif" alt="29_3_R2_equation">
Here, SSR = Sum Square of Residuals(the squared difference between the predicted and the average value)
&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;SST = Sum Square of Total(the squared difference between the actual and average value)
The above equation can be easily understood by the following illustration:
&nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp;&nbsp;<img data-filename="3_Evaluating_Regression_models.png" style="width: 560px;" src="/uploads/tutorials/2019/08/18_3_Evaluating_Regression_models.png">
Here the green line represents the regression line and the red line represents the average line. The differences in data points from these lines are taken in the equation.
Usually, the value of R^2 lies between 0 to 1(it can be negative if the regression line somehow has a worse fit than the average!). The closer its value to one, the better your model is. This is because either your regression line has well fitted the dataset or the data points are distributed with low variance. Which lessens the value of the Sum of Residuals. Hence, the equation gets closer to one.<h4>Adjusted R-squared</h4> There is a drawback of R^2 &nbsp;that it improves every time when we add new variables in the model.
Think about it, whenever you add a new variable there can be two circumstances, either the new variable improves your model or not. When the new variable improves your model then it is ok. But what if it does not improve your model? Then the problem occurs. The value of &nbsp;R^2 keeps on increasing with the addition of more independent variables even though they may not have a significant impact on the prediction.
To solve this pitfall, an Adjusted R^2 value is used instead of R^2 value. The mathematical representation for Adjusted &nbsp;R^2 &nbsp;is-
&nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp;&nbsp;<img data-filename="2_Evaluating_Regression_model.png" style="width: 780px;" src="/uploads/tutorials/2019/08/18_2_Evaluating_Regression_model.png"> 
Adjusted R^2 will penalize the model whenever you add a new variable to it. From the equation, you can understand that clearly. Whenever you add a new variable, the value of &nbsp;R^2 &nbsp;increases and it also increases the denominator( n - p - 1 ) on the left of the equation. As the denominator increases, it increases the value of 1 - &nbsp;R^2 on the left of the equation. Which in turn decreases the value of Adjusted R^2. Hence, using an Adjusted R^2 value you can better understand the effect of the additional variables to your model.
Note: Adjusted &nbsp;R^2 is greatly helpful when your dataset contains more features and you need to choose the most effective features to train your model.
<h5>Which Regression Model is the Best?&nbsp;</h5>
Well, this is subjective to your dataset and the model you choose. Each machine learning model solves a problem with a different objective using a different dataset. Hence, you must understand the context of using that model before choosing a metric.

4 Best Metrics for Evaluating Regression Model Performance

Classification: Classification is a machine learning task of predicting the value of a categorical variable(target or class). This is done by building a modal based on one or more numerical and categorical variables( predictors, attributes or features). It is considered an instance of supervised learning.
 
Classification is the problem of identifying to which of a set of categories a new observation belongs, on the basis of training data containing observations. Classification models include linear models like Logistic Regression, SVM, and nonlinear ones like K-NN, Kernel SVM, and Random Forests.
Now, we will learn how to implement the following Machine Learning Classification models:
<ol><li>
 Logistic Regression
 </li>
 <li>
 K-Nearest Neighbors (K-NN)
 </li>
 <li>
 Support Vector Machine (SVM)
 </li>
 <li>
 Kernel SVM
 </li>
</ol>

Classification

<img data-filename="logistic regression.jpg" style="width: 700px;" src="/uploads/tutorials/2020/08/10_logistic_regression.jpg"> In this article, we will go through the concept of logistic regression, a simple classification algorithm. Then we will implement the algorithm in Python.
Logistic Regression Intuition:
Logistic Regression is the appropriate regression analysis to solve binary classification problems( problems with two class values yes/no or 0/1). This algorithm analyzes the relationship between a dependent and independent variable and estimates the probability of an event to occur. Like other regression models, it is also a predictive model. But there is a slight difference. While other regression models provide continuous output, Logistic Regression is used to model the probability of a certain class or event existing such as pass/fail, win/lose, alive/dead or healthy/sick.
A good example can be finding the probability of getting cancer(yes/no) by a person for smoking for some years based on the dataset of people containing their smoking period, age, and the condition(having cancer or not).
How this Algorithm Works?
If you remember the regression, you can understand that in regression, we use a function to predict the probability of an event to occur. In logistic regression, the idea is the same but with that function, we combine another function named sigmoid or logistic function to find the probability. You can better understand from the following illustration- &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp;&nbsp;<img src="/uploads/tutorials/2018/09/21_log_1.png" alt="21_log_1" style="width: 50%;"> 
Top of the illustration you can see the original regression equation(at left) and the resulting regression line(at the right of the top). And when we combine it with the sigmoid function we get the logistic equation(in the green box at the bottom). And the resulting slope is shown at the bottom right.
Well, with this logistic function you will get the probability of an event to occur like the probability of buying a car by a person of a certain age.
<img src="/uploads/tutorials/2018/09/21_log_2.png" alt="21_log_2">
Here, you can see that people of a lower age(between 20 to 30) are less likely to buy a car(between 0.7% to 23%) whereas people of higher ages have more probability.
But wait! We are doing classification and we want the probability of people buying a car or not(yes/no values) but here we get a continuous probability. So what would we do is that we will take a threshold point(like 50% or 0.5) in the graph and based on that line we will calculate the probability.
<img src="/uploads/tutorials/2018/09/21_log_3.png" alt="21_log_3"> 
Here you can see we take a threshold point(50% or 0.5) where anything under that probability classified as a 0 or no value and above that line the probability is classified as 1 or yes.
This way we can use a regression function to solve classification problems.
Logistic Regression in Python : 
Now we will implement this algorithm in Python. Here we take a dataset containing the Age, Salary, and Action(yes/no value) of purchasing a car. Now our task is to classify a person in terms of his Age and Salary whether he/she is supposed to buy the car.
You can download the dataset from <a href="https://www.dropbox.com/s/sj2r3og9br7z08j/Social_Network_Ads.csv?dl=0" target="_blank">here.</a>
First of all, we import essential libraries. You will get the code in<a href="https://colab.research.google.com/drive/1k-vxpiLyQX88gjSsGt1iRUb7PuJTdxtl?usp=sharing" target="_blank"> Google Colab</a> also.<pre># Importing Essential Libraries import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
</pre>Now, we will import the dataset to our program.<pre># Importing the Dataset 
dataset = pd.read_csv('Social_Network_Ads.csv')
</pre>&nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp;<img src="/uploads/tutorials/2019/06/20_4_Logistic_Regression_Dataset.png" alt="20_4_Logistic_Regression_Dataset"> 
In this dataset, the Age and EstimatedSalary column are independent variables and the last column Purchased&nbsp;is the dependent variable. The last column contains the values 0 or 1. It means it provides the output like yes or no.
Now we take the indexes of Age and EstimatedSalary as our independent variable matrix. And take the Purchased column in the dependent variable vector.<pre>X = dataset.iloc[:, [2, 3]].values
y = dataset.iloc[:, 4].values
</pre>Now we split the dataset into a training set and a test set. For this, we take the test size=0.25%. And execute it. After execution, we get 300 training sets and 100 test sets.<pre># Splitting the Dataset into Training and Test Set 
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.25, random_state = 0)
</pre>Now, we will do feature scaling. To transform the x_train matrix object to scale, we use the fit_transform method.<pre># Scaling the Datasets
from sklearn.preprocessing import StandardScaler
sc = StandardScaler()
X_train = sc.fit_transform(X_train)
X_test = sc.transform(X_test)
</pre>
&nbsp;Now, we fit a logistic regression to the training set. We use the linear model library to import the class LogisticRegression. Then we create the classifier object and call that object.<pre># Fitting the Datataset with Regression Class 
from sklearn.linear_model import LogisticRegression
classifier = LogisticRegression(random_state = 0)
classifier.fit(X_train, y_train)
</pre>Note: Here we set the random_state to zero so that the result in our program and yours remain the same.
Well, we have come to the final part of the algorithm. Let's create a variable to predict the result.<pre># Predicting the output 
y_pred = classifier.predict(X_test)
</pre>
Now, we will see how good our model is to predict the values. Let's evaluate our model using the confusion matrix.<pre># Building the Confusion Matrix 
from sklearn.metrics import confusion_matrix
cm = confusion_matrix(y_test, y_pred)
</pre>
&nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp;<img src="/uploads/tutorials/2019/06/20_5_Logistic_Regression_Confusion_Matrix.png" alt="20_5_Logistic_Regression_Confusion_Matrix"> 
Here the output shows us that the model predicted 89 (65 + 24) correct and 11(8 + 3) incorrect values. So the accuracy of the model is 89%, pretty impressive!
Now we will visualize the result of our model.<pre># Visualising the Test set results from matplotlib.colors import ListedColormap X_set, y_set = X_test, y_test X1, X2 = np.meshgrid(np.arange(start = X_set[:, 0].min() - 1, stop = X_set[:, 0].max() + 1, step = 0.01), &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp;np.arange(start = X_set[:, 1].min() - 1, stop = X_set[:, 1].max() + 1, step = 0.01)) plt.contourf(X1, X2, classifier.predict(np.array([X1.ravel(), X2.ravel()]).T).reshape(X1.shape), &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp;alpha = 0.75, cmap = ListedColormap(('red', 'green'))) plt.xlim(X1.min(), X1.max()) plt.ylim(X2.min(), X2.max()) for i, j in enumerate(np.unique(y_set)): &nbsp; &nbsp; plt.scatter(X_set[y_set == j, 0], X_set[y_set == j, 1], &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; c = ListedColormap(('red', 'green'))(i), label = j) plt.title('Logistic Regression (Test set)') plt.xlabel('Age') plt.ylabel('Estimated Salary') plt.legend() plt.show()</pre>
&nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp;&nbsp;<img src="/uploads/tutorials/2018/09/21_log_6.png" alt="21_log_6">
Here the graph shows us the classification of purchasing a car or not based on various Ages and EstimatedSalary.

A Beginners Guide to Logistic Regression(with Example Python Code)

K-Nearest Neighbor in 4 Steps(Code with Python & R)

Support Vector Machine is one of the popular machine learning algorithms. I assume you have already learned the other classification algorithms like logistic regression and Naive Bayes. If you have not learned them I want you to check them before diving into SVM. Why? Because having a good knowledge of other simple classification algorithms will help you understand SVM better.In this tutorial, we will learn the Support Vector Machine algorithm in detail. Then we will implement a Support Vector Machine in Python.
<h4>What is Support Vector Machine?</h4>Support Vector Machine is a supervised machine learning algorithm. It can be used in both classification and regression problems. Inherently, it&nbsp;is a discriminative classifier. Given a set of labeled data points, an SVM tries to separate the data points into different output classes. It does so by finding an optimal hyperplane that distinctly classifies the data points into an N-dimensional space(N - the number of features).&nbsp;Before getting to the working principle of SVM, first, we need to understand some key definitions.<h5>What is a Hyperplane in SVM?</h5>
A hyperplane is defined as an n-1 dimensional Euclidean space that separates an n-dimensional Euclidean space into two disconnected parts or classes. The "optimal" hyperplane is one that maximizes the margin between the two classes, which means the distance of the hyperplane is equal from both the nearest data points of these two classes.In a two dimensional space, a hyperplane is a line that optimally divides the data points into two different classes. In three dimensions, a hyperplane is a 2D plane. In other higher dimensions, the hyperplane would take more complex shapes.<h5>What is a Support Vector in SVM?</h5>Support vectors are those two data points supporting the decision boundary(the data points which have the maximum margin from the hyperplane). An SVM always try to those two data points from different classes that are the closest to each other. These support vectors are the keys to draw an optimal hyperplane by SVM.&nbsp; In SVM, the set of input and output data are treated as vectors. This is because when the data is a higher-dimensional space(more than two dimensions), the classes cannot be represented as single data points, so they must be represented as vectors. And that's how it's got the name "Support Vector Machine".
<h4>How Does Support Vector Machine Work?</h4>
In the above, we got an intuitive idea of SVM. Now, we will see how the algorithm actually separates the classes. There can be two scenarios for an SVM depending on the nature of data. Data can be of two types- linearly separable or non-linearly separable. Let's understand the working procedure of SVM for both cases.Scenario 1: Data is linearly separableTo see what data is linearly separable, consider the following data plot-
<img src="/uploads/tutorials/2019/07/11_SVM_1.png" alt="11_SVM_1">Here the data is linearly separable because you can separate them into two classes just with a line. This line is known as the hyperplane in sense of and SVM. As we discussed earlier, SVM will find an optimal hyperplane that will separate the data into two "distinct" classes. This line can be drawn anywhere on the plane-
<img src="/uploads/tutorials/2019/07/11_SVM_2.png" alt="11_SVM_2"> 
 
In the above, any of the lines can separate the classes. But we need to take the optimal one, right? Here where the Support vectors come into play. SVM will find those two boundary data points or support vectors. These support vectors should be at a maximum margin from the optimal hyperplane.&nbsp; 
<img src="/uploads/tutorials/2019/07/11_SVM_3.png" alt="11_SVM_3"> 
This illustration tells us everything. You see the SVM finds the two closest support vectors and separates the classes with the optimal hyperplane.
Scenerio 2: Data is not linearly separableWhat if our data is in a more complex shape that they can not be linearly separable? Look at the following illustration-<img style="width: 466px;" data-filename="svm_5.png" src="/uploads/tutorials/2020/07/23_svm_5.png"> 
You see clearly there are two classes. But we can not separate them(you may try splitting with a knife!). Jokes apart, we can not separate them as the data is not linearly separable. But SVM can. What it does in this sense that it takes the data into a higher dimension. In a higher dimension, the data will be in different shapes and hence can be linearly separable.<img style="width: 746px;" data-filename="svm_6.png" src="/uploads/tutorials/2020/07/23_svm_6.png">You can see, taking the data into three-dimensional space, they become linearly separable by a 2D hyperplane. SVM creates a mapping function that elevates the data into a higher dimension. There it tries to find the optimal hyperplane. Recall how SVM finds it in the previous example. Then it projects back the data into its original dimension. Now, the data is well separated into two distinctive classes.<img style="width: 1046px;" data-filename="svm_7.jpg" src="/uploads/tutorials/2020/07/23_svm_7.jpg"> This is the whole idea of working with non-linear data. These mapping functions are made of special mathematical functions called the kernel trick.<h4>SVM Kernel Explained</h4>As we have seen, we can separate non-linearly separable data by taking them into a higher dimension. In our example, we need to map the data into just one dimension higher. But in most cases, we need to take higher dimensions to make the data linearly separable. Now, think about how much the computation cost would be to take the data into higher dimensions and remap them into the original dimensional? The operation will be costly.This is where the kernel trick comes into play. It allows us to calculate the data into a higher-dimensional space still remaining in our original feature space.&nbsp;In simple terms, Kernel Tricks are functions that apply some complex mathematical operations on the lower-dimensional data points and convert them into higher dimensional space.&nbsp; Then finds out the process of separating the data points based on the labels and outputs we have defined. This is less expensive and fast.<h5>Different Types of Kernels in SVM</h5>There are many types of kernels are used in SVM. Some of the common kernels are-<ul><li>Linear Kernel</li><li>Polynomial Kernel&nbsp;</li><li>Radial Basis Function of RBF Kernel</li><li>Sigmoid Kernel</li><li>Gaussian Kernel</li></ul><h5>Which Kernel is Best for SVM?</h5>There is no rule of thumb for a standard kernel in SVM. The choice of a kernel is data specific. Sometimes linear kernel works well for the data. If not, then you might go with Polynomial or Gaussian kernels. Though we can not say how good a kernel will be before using a kernel, in practice, the Gaussian kernel is the most widely used kernel. It works extremely well for well-behaved data i.e. data with no or less noise. For special-purpose problems or domains, you need to use more customized kernels. For instance, a graph kernel might be good when you want to classify graphs in a network or a string kernel is a good option for working with genetic data.
<h4>Support Vector Machine in Python</h4>Now we will implement this algorithm in Python. For this task, we will use the dataset Social_Network_Ads.csv. Let's have a glimpse of that dataset.
&nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp;&nbsp;<img alt="A+hVT3cdswwlAAAAAElFTkSuQmCC" src="/uploads/tutorials/2019/07/11_"> 
This dataset contains the buying decision of a customer based on gender, age and salary. Now, using SVM, we need to classify this dataset to predict the decision for unknown data points.
You can download the whole dataset from <a href="https://www.dropbox.com/s/sj2r3og9br7z08j/Social_Network_Ads.csv?dl=0" target="_blank">here.</a>
 
First of all, we need to import the essential libraries to our program. You will get the code in <a href="https://colab.research.google.com/drive/1scnad6s_g_smSBorguvNkKwsdrc955MZ?usp=sharing" target="_blank">Google Colab</a> also.<pre>import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
</pre>Now, lets import the datset.<pre>dataset = pd.read_csv('Social_Network_Ads.csv')</pre>
In the dataset, the Age and EstimatedSalary columns are independent and the Purchased column is dependent. So we will take both the Age and EstimatedSalary in our feature matrix and the Purchased column in the dependent variable vector.<pre>X = dataset.iloc[:, [2, 3]].values
y = dataset.iloc[:, 4].values
</pre>Now, we will split our dataset in training and test sets.<pre>from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.25, random_state = 0)
</pre> We need to scale our dataset for getting a more accurate prediction.<pre>from sklearn.preprocessing import StandardScaler
sc = StandardScaler()
X_train = sc.fit_transform(X_train)
X_test = sc.transform(X_test)
</pre>Well, its time to fit the SVM algorithm to our training set. For this, we use the SVC class from the ScikiLearn library. <pre>from sklearn.svm import SVC
classifier = SVC(kernel = 'linear', random_state = 0)
classifier.fit(X_train, y_train)
</pre>Note: Here kernel specifies the type of algorithm we are using. You will know about it in detail in our <a href="http://www.aionlinecourse.com/tutorial/machine-learning/kernel-svm" target="_blank">Kernel SVM</a>&nbsp;tutorial. For simplicity, here we choose the linear kernel.Our model is ready. Now, let's see how it predicts for our test set.<pre>y_pred = classifier.predict(X_test)</pre>To see how good is our SVM model is, let's calculate the predictions made by it using the confusion matrix.<pre>from sklearn.metrics import confusion_matrix cm = confusion_matrix(y_test, y_pred)&nbsp;</pre>The output of the confusion matrix will be&nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp;<img data-filename="5_SVM.png" style="width: 212px;" src="/uploads/tutorials/2019/07/11_5_SVM.png"><h4>Visualizing Support Vector Machine in Python</h4>Now, let's visualize our test set result.<pre># Visualising the Test set results from matplotlib.colors import ListedColormap X_set, y_set = X_test, y_test X1, X2 = np.meshgrid(np.arange(start = X_set[:, 0].min() - 1, stop = X_set[:, 0].max() + 1, step = 0.01), &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp;np.arange(start = X_set[:, 1].min() - 1, stop = X_set[:, 1].max() + 1, step = 0.01)) plt.contourf(X1, X2, classifier.predict(np.array([X1.ravel(), X2.ravel()]).T).reshape(X1.shape), &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp;alpha = 0.75, cmap = ListedColormap(('red', 'green'))) plt.xlim(X1.min(), X1.max()) plt.ylim(X2.min(), X2.max()) for i, j in enumerate(np.unique(y_set)): &nbsp; &nbsp; plt.scatter(X_set[y_set == j, 0], X_set[y_set == j, 1], &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; c = ListedColormap(('red', 'green'))(i), label = j) plt.title('SVM (Test set)') plt.xlabel('Age') plt.ylabel('Estimated Salary') plt.legend() plt.show()</pre>The graph will like the following
<img src="/uploads/tutorials/2018/09/21_svmp_4.png" alt="21_svmp_4">From the above graph, we can see that our model tries to find the optimal line that separates the data points accurately.This tutorial only explains SVM in two-dimensional space, in the next tutorial we will see SVM in higher dimensional spaces.
Multiclass SVM ExplanationSupport Vector Machines are inherently binary classifiers. This is why it is called one of classifier. But in many cases, especially in text classification, one of classification problems are rare. For example, take some text data like China, Coffe, UK, where they can be relevant to many topics. However,&nbsp; to perform multiclass classification with SVM, we can apply one of the following strategies-<ul><li>Build a one-versus-rest classifier or commonly known as the One-Versus-All(OVA) classifier. Then choose the class which classifies the test data with highest margin. The training time is higher in this case as you have to take all the training data for one classifier.</li><li>Build a set of OVA classifiers. Then choose the class that is selected by the highest number of classifiers. This approach reduces the training time since the training data is distributed to each classifier.</li></ul>The two above mentioned methods are quite general and not a very elegant approach to solving multiclass problems. A better approach is to build a multiclass SVM which could naturally deal with multiclass problems.The construction of a multiclass SVM is quite complex and beyond the scope of this tutorial. I suggest you check this&nbsp;<a href="https://www.cs.cornell.edu/people/tj/svm_light/svm_multiclass.html">implementation</a>&nbsp;to learn more about the multiclass support vector machines.<h4>What is the Difference Between SVM and LinearSVC?</h4>LinearSVC stands for Linear Support Vector Classification. It is similar to SVC in terms of the kernel parameter(when kernel='linear'). But the difference is in implementation. SVC implemented in terms of libsvm whereas LinearSVC is implemented in terms of liblinear. It makes it more flexible in the choice of penalties and loss functions. This class supports both dense and sparse inputs. The multiclass classification is handled by using one-vs-all(OVM) strategy.Talking about performance, LinearSVC can perform better than SVC when there is a large number of data. <h4 style='font-family: -apple-system, BlinkMacSystemFont, "Segoe UI", Roboto, Oxygen, Ubuntu, Cantarell, "Fira Sans", "Droid Sans", "Helvetica Neue", sans-serif; color: rgb(0, 0, 0);'>Advantages and Disadvantages of Support Vector Machine</h4>There are some key benefits to choose a support vector machine for classification. There are some drawbacks as well. Let's talk about them-The key advantages are-<ul><li>SVM works really well with high dimensional data. If your data is in higher dimensions, it is wise to use SVM.</li><li>For data with a clear margin of separations, SVM works relatively well.</li><li>When data has more features than the number of observations, SVM is one of the best algorithms to use.</li><li>As a discriminative model, it need not memorize anything about data. Therefore, it is memory efficient.&nbsp;</li></ul>Some drawbacks are-<ul><li>It is a bad option when the data has no clear margin of separation i.e. the target class contains overlapping data points.</li><li>It does not work well with large data sets.</li><li>For being a discriminative model, it separates the data points below and above a hyperplane. So, you will not get any probabilistic explanation of the output.</li><li>It is hard to understand and interpret SVM as its underlying structure is quite complex.</li></ul><p style='word-break: break-word; hyphens: none; color: rgb(33, 37, 41); font-family: -apple-system, BlinkMacSystemFont, "Segoe UI", Roboto, "Helvetica Neue", Arial, "Noto Sans", sans-serif, "Apple Color Emoji", "Segoe UI Emoji", "Segoe UI Symbol", "Noto Color Emoji";'> <h4 style='word-break: break-word; hyphens: none; color: rgb(33, 37, 41); font-family: -apple-system, BlinkMacSystemFont, "Segoe UI", Roboto, "Helvetica Neue", Arial, "Noto Sans", sans-serif, "Apple Color Emoji", "Segoe UI Emoji", "Segoe UI Symbol", "Noto Color Emoji";'>Final Thoughts</h4><p style='word-break: break-word; hyphens: none; color: rgb(33, 37, 41); font-family: -apple-system, BlinkMacSystemFont, "Segoe UI", Roboto, "Helvetica Neue", Arial, "Noto Sans", sans-serif, "Apple Color Emoji", "Segoe UI Emoji", "Segoe UI Symbol", "Noto Color Emoji";'>The tutorial is designed in a way to provide all the essential concepts you need to learn about Support Vector Machine. We have learned what SVM is and how it works. We understood different angles of SVM for linear and non-linear data. Then we implemented it in python. We also tried to understand the multiclass classification with SVM. We further discussed the advantages and disadvantages of SVM.&nbsp;<p style='word-break: break-word; hyphens: none; color: rgb(33, 37, 41); font-family: -apple-system, BlinkMacSystemFont, "Segoe UI", Roboto, "Helvetica Neue", Arial, "Noto Sans", sans-serif, "Apple Color Emoji", "Segoe UI Emoji", "Segoe UI Symbol", "Noto Color Emoji";'>This article is a simple yet intuitive explanation of SVM. You should read more mathematical theories behind SVM to get a deep understanding of this powerful algorithm. Hope this article could help you make this thing clearer. What do you think? Let me know in the comments.<p style='word-break: break-word; hyphens: none; color: rgb(33, 37, 41); font-family: -apple-system, BlinkMacSystemFont, "Segoe UI", Roboto, "Helvetica Neue", Arial, "Noto Sans", sans-serif, "Apple Color Emoji", "Segoe UI Emoji", "Segoe UI Symbol", "Noto Color Emoji";'>Happy Machine Learning!

Support Vector Machine(SVM) Made Easy with Python

<img data-filename="support vector machine.jpg" style="width: 1046px;" src="/uploads/tutorials/2020/08/10_support_vector_machine.jpg"> In this tutorial, we are going to introduce the Kernel Support Vector Machine and how to implement it in Python.
Kernel SVM Intuition: 
In the previous Support Vector Machine tutorial, we implemented SVM for the following scenario.
<img src="/uploads/tutorials/2019/07/11_Kernel_SVM_1.png" alt="11_Kernel_SVM_1"> 
Here the data points are linearly separable. That means we can separate the data points with a straight line.
<img src="/uploads/tutorials/2019/07/1562875590_11_SVM_3.png" alt="1562875590_11_SVM_3"> 
 
But what if we have data points like the following
&nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp;&nbsp;<img src="/uploads/tutorials/2019/07/11_21_kernel_svm_1.png" alt="11_21_kernel_svm_1"> 
Here the data points do not look like the previous data points(though both in the same dimensional space). As we can see they can not be separated into two distinctive classes with a straight line. This is because these data points are not linearly separable.
So what can we do to make them linearly separable so that we can apply the SVM algorithm to the data point?&nbsp;
Well, we can do one thing, that is we can take the data points in a higher-dimensional space where they become linearly separable. To get a clear idea of this concept, lets look at the following illustration.
 
&nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp;<img src="/uploads/tutorials/2019/07/11_21_kernel_svm_3.png" alt="11_21_kernel_svm_3"> 
 
Here we used a mapping function(a function that maps the lower-dimensional data points in a higher-dimensional space), that elevates our data points into a higher dimensional space where they become linearly separable. And we find a hyperplane that classifies the data points into two distinctive classes. Then we will project our data points to the initial dimensional space using another function.
<img src="/uploads/tutorials/2019/07/11_Kernel_SVM_5.jpg" alt="11_Kernel_SVM_5"> 
 
This is the whole idea of separating non-linear data points. In SVM, we do this by a special method or function called Kernel Trick.
 
In simple terms, Kernel Tricks are functions that apply some complex mathematical operations on the lower-dimensional data points and convert them into higher dimensional space, then find out the process of separating the data points based on the labels and outputs you have defined.
There are many kernel tricks used in SVM. Some most used kernels are- the Gaussian RBF Kernel, Polynomial Kernel, Sigmoid Kernel, etc.
Here we choose the Gaussian RBF Kernel.
 
The Kernel trick:&nbsp;Here we choose the Gaussian RBF Kernel function.
&nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp;&nbsp;<img src="/uploads/tutorials/2018/09/21_kernel_svm_4.png" alt="21_kernel_svm_4"> 
 
And using the simplified formula of this Kernel Function stated above, we can find the classification of data points like the following.
 
&nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp;<img src="/uploads/tutorials/2018/09/21_kernel_svm_9.png" alt="21_kernel_svm_9">
 
 
 
Kernel SVM in python:&nbsp;Now, we will implement this algorithm in Python. For this task, we will use the Social_Network_Ads.csv dataset. Let's have a glimpse of that dataset.&nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp;&nbsp;<img data-filename="4_SVM.png" style="width: 500px;" src="/uploads/tutorials/2019/07/11_4_SVM.png"> 
This dataset contains the buying decision of a customer based on gender, age and salary. Now, using SVM, we need to classify this dataset to predict the decision for unknown data points.
You can download the whole dataset from&nbsp;<a href="https://www.dropbox.com/s/sj2r3og9br7z08j/Social_Network_Ads.csv?dl=0">here.</a>
First of all, we need to import essential libraries. You will get the code in <a href="https://colab.research.google.com/drive/1y70z2xIkOe-yXe8gBoPDQ2WCp8rSbf5Z?usp=sharing" target="_blank">Google Colab</a> also.<pre>import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
</pre>Then we will import the dataset.<pre>dataset = pd.read_csv('Social_Network_Ads.csv')</pre>
Now, let's divide the features of the dataset into feature matrix X and dependent variable vector y.<pre>X = dataset.iloc[:, [2, 3]].values
y = dataset.iloc[:, 4].values</pre>
Then we will make training and test sets.<pre>from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.25, random_state = 0)
</pre>Let's scale the training and test sets. <pre>from sklearn.preprocessing import StandardScaler sc = StandardScaler() X_train = sc.fit_transform(X_train) X_test = sc.transform(X_test)</pre>It's time to fit SVC into our model. For this, we will use the SVC class from the ScikitLearn library.<pre>from sklearn.svm import SVC
classifier = SVC(kernel = 'rbf', random_state = 0)
classifier.fit(X_train, y_train)
</pre>We have built our model. Let's say how it predicts on the test set.<pre>y_pred = classifier.predict(X_test)</pre> 
We are going to visualize the predicted result.
<pre># Visualising the Test set results from matplotlib.colors import ListedColormap X_set, y_set = X_test, y_test X1, X2 = np.meshgrid(np.arange(start = X_set[:, 0].min() - 1, stop = X_set[:, 0].max() + 1, step = 0.01), &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp;np.arange(start = X_set[:, 1].min() - 1, stop = X_set[:, 1].max() + 1, step = 0.01)) plt.contourf(X1, X2, classifier.predict(np.array([X1.ravel(), X2.ravel()]).T).reshape(X1.shape), &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp;alpha = 0.75, cmap = ListedColormap(('red', 'green'))) plt.xlim(X1.min(), X1.max()) plt.ylim(X2.min(), X2.max()) for i, j in enumerate(np.unique(y_set)): &nbsp; &nbsp; plt.scatter(X_set[y_set == j, 0], X_set[y_set == j, 1], &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; c = ListedColormap(('red', 'green'))(i), label = j) plt.title('Kernel SVM (Test set)') plt.xlabel('Age') plt.ylabel('Estimated Salary') plt.legend() plt.show()</pre>
&nbsp; The above code will generate the following graph.&nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp;&nbsp;<img src="/uploads/tutorials/2018/09/21_kernel_svm_13.png" alt="21_kernel_svm_13">
We can see that the graph looks different than that of the previous SVM result. This is because we modeled the data points in a higher-dimensional space.

Kernel SVM for Dummies(with Python Code)

Naive Bayes Classification Just in 3 Steps(with Python Code)

<img data-filename="decision tree classification.jpg" style="width: 1046px;" src="/uploads/tutorials/2020/08/12_decision_tree_classification.jpg"> In this article, we are going to understand the concept of Decision Tree algorithm for classification and then we will implement it in Python. Decision Tree Classification: This Classification is based on the decision tree structure. A decision tree is a form of a tree or hierarchical structure that breaks down a dataset into smaller and smaller subsets. At the same time, an associated decision tree is incrementally developed. The tree contains decision nodes and leaf nodes. The decision nodes are those nodes represent the value of the input variable(x). It has two or more than two branches. The leaf nodes contain the decision or the output variable(y). The decision node that corresponds to the best predictor becomes the topmost node and called the root node.
<img src="/uploads/tutorials/2019/07/18_2_decision_tree.png" alt="18_2_decision_tree"> 
 
 
When You Should Choose a Decision Tree?
Assume you have a dataset where the data points are randomly distributed. Consider the following illustration.
&nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp;&nbsp;<img src="/uploads/tutorials/2019/07/1563466188_18_2_decision_tree.png" alt="1563466188_18_2_decision_tree"> 
For a randomly distributed dataset like this, you should not go for the other classification algorithm like SVM, K-means, or Naive Bayes. As more randomness in data will create more entropy, you must choose an algorithm that minimizes the entropy and maximize the information gain. In that context, you should implement a Decision Tree for classification.
Entropy is the measure of randomness or impurity contained in a dataset. Information gain is the opposite of entropy that measures the decrease in entropy.
 
How does the Algorithm Work?
This algorithm works based on maximizing the information gain in the groups of data points. That means it splits the data points into optimal parts(subtree) in such a way that it contains as much as information and less randomness. It selects the best attributes using the Attribute Selection Measures to split the data. For the above data points, it would split them in the following way.
&nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp;<img src="/uploads/tutorials/2019/07/18_3_decision_tree.jpg" alt="18_3_decision_tree"> 
Then it makes the attribute a decision node and breaks the dataset into smaller subsets(subtree). It repeats the process recursively for each child node until there is no more remaining attributes or no more instances to add to the tree.
For the above dataset, it will make a tree like this.
&nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp;<img src="/uploads/tutorials/2019/07/18_4_decision_tree.png" alt="18_4_decision_tree"> 
 
Then to classify a new data point, it will traverse the tree and try to match that point to one of the decision nodes. If it reaches that node, it returns the leaf node value for that data point.
It is quite a simple method but at the same time, it lies in the foundation of some of the more modern and powerful method of machine learning.
 
Decision Tree Classification in python: Now, we will implement the above algorithm in Python. For this task, we will use Social_Network_Ads.csv dataset. Lets have a glimpse of that dataset.&nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp;&nbsp;<img data-filename="17_5_Decision_tree.png" style="width: 500px;" src="/uploads/tutorials/2019/07/18_17_5_Decision_tree.png">o 
&nbsp;You can download the whole dataset from <a href="https://www.dropbox.com/s/sj2r3og9br7z08j/Social_Network_Ads.csv?dl=0" target="_blank">here.</a>First of all, we will import the libraries. You will get the full code in <a href="https://colab.research.google.com/drive/1YcJ-1BH6Psy5tMh33viF945_2zPFhWS9?usp=sharing" target="_blank">Google Colab</a> also.<pre>import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
</pre>Then we will import the dataset into our program and divide the attributes into Feature matrix and dependent variable vectors. Here the Age and EstimatedSalary are the independent attributes, so we will put them into the Feature matrix and the Purchased column into the dependent variable vector.<pre># Importing the dataset
dataset = pd.read_csv('Social_Network_Ads.csv')
X = dataset.iloc[:, [2, 3]].values
y = dataset.iloc[:, 4].values</pre>Now, we will split the dataset into training and test sets.<pre># Splitting the dataset into the Training set and Test set
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.25, random_state = 0)
</pre>We need to scale our dataset for a more accurate prediction.<pre># Feature Scaling
from sklearn.preprocessing import StandardScaler
sc = StandardScaler()
X_train = sc.fit_transform(X_train)
X_test = sc.transform(X_test)
</pre>It's time to fit the Decision tree algorithm to our dataset.<pre># Fitting Decision Tree Classification to the Training set
from sklearn.tree import DecisionTreeClassifier
classifier = DecisionTreeClassifier(criterion = 'entropy', random_state = 0)
classifier.fit(X_train, y_train)
</pre>
Note: Here criterion is the parameter that measures the quality of a split. We choose 'entropy' for the information gain.We have built our model. Now, we will predict the result.<pre># Predicting the Test set results
y_pred = classifier.predict(X_test)</pre>To learn how our model performed on the dataset, we will build a confusion matrix.<pre># Making the Confusion Matrix
from sklearn.metrics import confusion_matrix
cm = confusion_matrix(y_test, y_pred)</pre> After executing, the output of the confusion matrix would look like this.
&nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp;<img data-filename="6_Decision_Tree.png" style="width: 224px;" src="/uploads/tutorials/2019/07/18_6_Decision_Tree.png">
 
Now, we have come to the most fun and exciting part. We will visualize both the training set and test set results.&nbsp;<pre># Visualising the Training set results
from matplotlib.colors import ListedColormap
X_set, y_set = X_train, y_train
X1, X2 = np.meshgrid(np.arange(start = X_set[:, 0].min() - 1, stop = X_set[:, 0].max() + 1, step = 0.01),
 np.arange(start = X_set[:, 1].min() - 1, stop = X_set[:, 1].max() + 1, step = 0.01))
plt.contourf(X1, X2, classifier.predict(np.array([X1.ravel(), X2.ravel()]).T).reshape(X1.shape),
 alpha = 0.75, cmap = ListedColormap(('red', 'green')))
plt.xlim(X1.min(), X1.max())
plt.ylim(X2.min(), X2.max())
for i, j in enumerate(np.unique(y_set)):
 plt.scatter(X_set[y_set == j, 0], X_set[y_set == j, 1],
 c = ListedColormap(('red', 'green'))(i), label = j)
plt.title('Decision Tree Classification (Training set)')
plt.xlabel('Age')
plt.ylabel('Estimated Salary')
plt.legend()
plt.show()
</pre><div> </div>
&nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp;<img src="/uploads/tutorials/2018/09/21_de_t_3.png" alt="21_de_t_3"> <pre># Visualising the Test set results
from matplotlib.colors import ListedColormap
X_set, y_set = X_test, y_test
X1, X2 = np.meshgrid(np.arange(start = X_set[:, 0].min() - 1, stop = X_set[:, 0].max() + 1, step = 0.01),
 np.arange(start = X_set[:, 1].min() - 1, stop = X_set[:, 1].max() + 1, step = 0.01))
plt.contourf(X1, X2, classifier.predict(np.array([X1.ravel(), X2.ravel()]).T).reshape(X1.shape),
 alpha = 0.75, cmap = ListedColormap(('red', 'green')))
plt.xlim(X1.min(), X1.max())
plt.ylim(X2.min(), X2.max())
for i, j in enumerate(np.unique(y_set)):
 plt.scatter(X_set[y_set == j, 0], X_set[y_set == j, 1],
 c = ListedColormap(('red', 'green'))(i), label = j)
plt.title('Decision Tree Classification (Test set)')
plt.xlabel('Age')
plt.ylabel('Estimated Salary')
plt.legend()
plt.show()</pre> 
&nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp;&nbsp;<img src="/uploads/tutorials/2018/09/21_de_t_4.png" alt="21_de_t_4"> 
Though the Decision Tree algorithm is good for classification of random data, it is sensitive to noisy data and has a tendency to overfit data. Even the small variance in data can result in different Decision Trees. So it is recommended to balance the dataset before fitting the algorithm to the dataset.

Decision Tree Classification for Dummies(with Python Code)

Random Forest is an ensemble learning technique. It builds a number of decision trees on the randomly selected data sample. Then it gets predictions from each tree and by means of majority voting, it selects the decision which gets the majority vote.
 
&nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp;<img src="/uploads/tutorials/2019/07/19_1_Random_Forest.jpg" alt="19_1_Random_Forest"> 
How does the Algorithm work?
As said earlier, this algorithm is based on decision trees. For a given dataset, it takes some random data points, builds decision trees one at a time around them. The number of trees is defined in the program. Then it comprises the predictions of all the decision trees. From the predictions, it chooses the best one which is predicted by the most number of trees.&nbsp;
 
The steps for Random Forest Algorithms are as follows-
 
STEP 1: Pick at random K data points from the Training set.&nbsp;
STEP 2: Build the Decision Tree associated with these K data points.&nbsp;
STEP 3: Choose the number Ntree of trees you want to build and repeat STEPS 1 &amp; 2&nbsp;
STEP 4: For a new data point, make each one of your Ntree trees predict the category to which the data points belongs, and assign the new data point to the category that wins the majority vote.
 
This simple ensemble technique gives astonishingly accurate predictions. This is because one decision tree may provide wrong predictions, but aggregating the decisions of a large number of trees will reduce the wrong predictions leading to more accurate predictions.
 
Now, we will implement this algorithm in Python.
 
Random Forest Classification in Python:
For this task, we will use the dataset named Social_Network_Ads.csv. This dataset contains the age, salary, and buying choice for a specific product of a number of customers through social network ads. Our task is to classify what will be the buying choice of a future customer upon given these features. Let's have a glimpse of that dataset
 
&nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp;&nbsp;<img src="/uploads/tutorials/2019/07/19_2_Random_Forest.png" alt="19_2_Random_Forest">.
You can download the whole dataset from <a href="https://www.dropbox.com/s/sj2r3og9br7z08j/Social_Network_Ads.csv?dl=0">here.</a>
 
First of all, we will import the essential libraries to our program. You will get the code in <a href="https://colab.research.google.com/drive/1tAByYVUHSIxznoKuyTMN1NLMU_k6FI1D?usp=sharing" target="_blank">Google Colab</a> also.<pre># Importing the libraries 
import numpy as np 
import matplotlib.pyplot as plt 
import pandas as pd</pre>
Then we will import the dataset into our program and divide the attributes into Feature matrix and dependent variable vectors. Here the&nbsp;Age&nbsp;and&nbsp;EstimatedSalary&nbsp;are the independent attributes, so we will put them into the Feature matrix and the&nbsp;Purchased&nbsp;column into the dependent variable vector.
 <pre># Importing the dataset 
dataset = pd.read_csv('Social_Network_Ads.csv') 
X = dataset.iloc[:, [2, 3]].values 
y = dataset.iloc[:, 4].values</pre>
Now, we will split the dataset into training and test sets. # Splitting the dataset into the Training set and Test set <pre>from sklearn.model_selection import train_test_split 
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.25, random_state = 0)
</pre>We need to scale our dataset for a more accurate prediction.<pre># Feature Scaling 
from sklearn.preprocessing import StandardScaler 
sc = StandardScaler() 
X_train = sc.fit_transform(X_train) 
X_test = sc.transform(X_test)</pre>
It's time to fit the Random Forest algorithm to our dataset.<pre># Fitting Random Forest Classification to the Training set 
from sklearn.ensemble import RandomForestClassifier 
classifier = RandomForestClassifier(n_estimators = 10, criterion = 'entropy', random_state = 0) 
classifier.fit(X_train, y_train)</pre>
Note: Here n_estimators defines the number of decision trees we want in our Random Forest.
We have built our model. Now, Lets see how it predicts on the test set.<pre># Predicting the Test set results 
y_pred = classifier.predict(X_test)</pre>
We could build the confusion matrix to see the accuracy of our model.<pre># Making the Confusion Matrix 
from sklearn.metrics import confusion_matrix 
cm = confusion_matrix(y_test, y_pred)</pre>
&nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp;&nbsp;<img data-filename="5_Radom_Forest.png" style="width: 244px;" src="/uploads/tutorials/2019/07/19_5_Radom_Forest.png"> We have come to the most exciting and fun part. Lets visualize the predictions of our model for training and test sets.<pre># Visualising the Training set results
from matplotlib.colors import ListedColormap
X_set, y_set = X_train, y_train
X1, X2 = np.meshgrid(np.arange(start = X_set[:, 0].min() - 1, stop = X_set[:, 0].max() + 1, step = 0.01),
 np.arange(start = X_set[:, 1].min() - 1, stop = X_set[:, 1].max() + 1, step = 0.01))
plt.contourf(X1, X2, classifier.predict(np.array([X1.ravel(), X2.ravel()]).T).reshape(X1.shape),
 alpha = 0.75, cmap = ListedColormap(('red', 'green')))
plt.xlim(X1.min(), X1.max())
plt.ylim(X2.min(), X2.max())
for i, j in enumerate(np.unique(y_set)):
 plt.scatter(X_set[y_set == j, 0], X_set[y_set == j, 1],
 c = ListedColormap(('red', 'green'))(i), label = j)
plt.title('Random Forest Classification (Training set)')
plt.xlabel('Age')
plt.ylabel('Estimated Salary')
plt.legend()
plt.show()</pre> &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp;&nbsp;<img data-filename="3_Random_Forest.png" style="width: 439px;" src="/uploads/tutorials/2019/07/19_3_Random_Forest.png"> <pre># Visualising the Test set results
from matplotlib.colors import ListedColormap
X_set, y_set = X_test, y_test
X1, X2 = np.meshgrid(np.arange(start = X_set[:, 0].min() - 1, stop = X_set[:, 0].max() + 1, step = 0.01),
 np.arange(start = X_set[:, 1].min() - 1, stop = X_set[:, 1].max() + 1, step = 0.01))
plt.contourf(X1, X2, classifier.predict(np.array([X1.ravel(), X2.ravel()]).T).reshape(X1.shape),
 alpha = 0.75, cmap = ListedColormap(('red', 'green')))
plt.xlim(X1.min(), X1.max())
plt.ylim(X2.min(), X2.max())
for i, j in enumerate(np.unique(y_set)):
 plt.scatter(X_set[y_set == j, 0], X_set[y_set == j, 1],
 c = ListedColormap(('red', 'green'))(i), label = j)
plt.title('Random Forest Classification (Test set)')
plt.xlabel('Age')
plt.ylabel('Estimated Salary')
plt.legend()
plt.show()</pre> &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp;&nbsp;<img data-filename="4_Random_Forest.png" style="width: 439px;" src="/uploads/tutorials/2019/07/19_4_Random_Forest.png">If you compare the results with a single <a href="http://www.aionlinecourse.com/tutorial/machine-learning/decision-tree-classification" target="_blank">Decision Tree classifier</a>, you must find that Random Forest tends to provide more accurate predictions.

Random forest Classification

Through this post, you are going to understand different metrics for the evaluation of classification models.
The Basics: False Positive and False Negative&nbsp;
Suppose your classification model predicts the probability of a person having cancer based on various features. Here the outcome is binary, either Yes or No. That means the person has cancer or not. That's simple. Well, as your model is not absolutely correct every time (it doesn't provide 100% accuracy), it will misjudge some events and thus provide the wrong outcome. If your model predicts that the person has cancer but in reality, he doesn't, then the outcome is a False Positive or Type I error. On the other hand, if the person does have cancer, but your model predicts No, then that is a False Negative or Type II error.&nbsp;
<img src="/uploads/tutorials/2019/07/21_1_Evaluating_Classification_model.png" alt="21_1_Evaluating_Classification_model"> 
Here the red points are the actual outcomes and the grey points are predicted outcomes. False-positive errors are less impactful so as False Negative errors. For example, if the model predicts the person doesn't have cancer while he actually has will have more impact than the prediction that tells the person has cancer but in reality does not.
Confusion Matrix:Confusion Matrix is the most commonly used metric for evaluating the performance of a classification model. It shows the number of correct and incorrect predictions made by a model compared to the actual outcomes(target value). It is an NxN matrix, where N is the number of target classes. i.e. the number of labels for predictions. It shows the number of False Positive(FP) and False Negative(FN) in the NxN grid.
&nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp;&nbsp;<img src="/uploads/tutorials/2019/07/21_5_Evaluating_classification_models.png" alt="21_5_Evaluating_classification_models"> 
Here
TP = True Positive, the actual and predicted outcomes are both positive
FP = False Positive, the predicted outcome is true but the target value is false
TN = True Negative, the actual and predicted outcome are both negative
FN = False Negative, the predicted outcome is negative but the target value is positive
 
Using the confusion matrix, we can calculate the accuracy rate of our models. Let's take an example.
<img src="/uploads/tutorials/2019/07/21_2_Evaluating_classification_model_LI.jpg" alt="21_2_Evaluating_classification_model_LI">
 Accuracy Paradox
The confusion matrix may lead to the wrong evaluation of models. This is known as the accuracy paradox. It happens when you stop your model to predict logically, which means you stop the model to learn. For example, let's say we have a model with the following confusion matrix.
<img src="/uploads/tutorials/2019/07/21_3_Evaluating_classification_model.png" alt="21_3_Evaluating_classification_model"> 
 
Let's say from now on we ask our model to predict only a false outcome that is a zero in the confusion matrix. Now see how the accuracy look like.
<img src="/uploads/tutorials/2019/07/21_4_Evaluating_classification_model.png" alt="21_4_Evaluating_classification_model"> 
In the second case, we can see that the accuracy of the model went up though the model was not actually doing any logical predictions.&nbsp;
Though easy to understand but Confusion matrix is not a good metric for model evaluation.&nbsp;
 
Cumulative Accuracy Profile(CAP) Curve
The cumulative accuracy profile (CAP) is used in data science to visualize the discriminative power of a model. The CAP of a model represents the cumulative number of positive outcomes along the y-axis versus the corresponding cumulative number of a classifying parameter along the x-axis. The CAP is distinct from the receiver operating characteristic(ROC), which plots the true-positive rate against the false-positive rate.
Let's take an example say we are contacting customers to sell some products. And we know that among our customers, 10% of them will buy our product. Now, if we build a model that helps us to classify which of the customers will respond to us if conducted.
Now how could we say that ours one is a good model?
<img src="/uploads/tutorials/2019/07/21_5_Evaluating_classsification_model.png" alt="21_5_Evaluating_classsification_model"> 
 
In the above illustration, we have plotted the scenario. First, we draw a random line from the probability we have known earlier( that 10% of our customers will respond). Now, if the area between the model's prediction line and the random line is substantially large, then we can say that this is a good model. If the area is small then the model should be considered as a poor model. Here the red line shows a good model comparable to the green line. The grey line above represents an ideal model. That is when we exactly know the customers who would buy our products.
&nbsp;
CAP Curve Analysis
We can easily calculate the goodness of our model from the CAP curve. For this, we first calculate the area between the perfect model line and the random line(aP). We also find the area between the good model line and the random line(aR). Then we take their ratio.
 
<img src="/uploads/tutorials/2019/07/21_6_Evaluating_classification_model.png" alt="21_6_Evaluating_classification_model"> 
 
This ratio is between 0 and 1. The more this ratio is closed to one, the better the model is. We can also intuitively decide the goodness of a model just by seeing it. Let's say we take a point on the X-axis(somewhere between 50%). From there we calculate the value on the Y-axis (represented as x).&nbsp;If the value of x is under 60%, the model is a worse one. If it lies between 60% to 70%, it is a poor model. If the accuracy is between 70% to 80%, it is a good model. Between 80% to 90% will be considered very good. If the model could hit an accuracy between 90% to 100%, you can consider it a too good model.
<img src="/uploads/tutorials/2019/07/21_7_Evaluating_Classification_model.png" alt="21_7_Evaluating_Classification_model">

Evaluating Classification Model performance

<img data-filename="clustering.jpeg" style="width: 500px;" src="/uploads/tutorials/2020/08/22_clustering.jpeg"> In this tutorial, we are going to understand K-means Clustering and implement the algorithm in Python<h4 style='font-family: -apple-system, BlinkMacSystemFont, "Segoe UI", Roboto, Oxygen, Ubuntu, Cantarell, "Fira Sans", "Droid Sans", "Helvetica Neue", sans-serif; color: rgb(0, 0, 0);'>What is Clustering?</h4>Clustering is an unsupervised learning algorithm. A cluster refers to groups of aggregated data points because of certain similarities among them. Clustering algorithms group the data points without referring to known or labeled outcomes.
There are commonly two types of clustering algorithms, namely K-means Clustering and Hierarchical Clustering. In this tutorial, we are going to understand and implement the simplest one of them- the K-means clustering.
<h4>What is K-means Clustering?&nbsp;</h4>This algorithm categorizes data points into a predefined number of groups K, where each data point belongs to the group or cluster with the nearest mean. Data points are clustered based on similarities in their features. The algorithm works iteratively to assign each data point to one of the K groups in such a way that the distance(i.e. Euclidian or Manhattan) between the centroid(i.e. the center of the cluster) of that group and the data point be small. The algorithm produces exactly K different clusters of the greatest possible distinction. 
&nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp;<img src="/uploads/tutorials/2019/07/23_1_K_means_clustering.png" alt="23_1_K_means_clustering"> 
<h4>How K-means Clustering Works?&nbsp;<span style='color: rgb(0, 0, 0); font-family: -apple-system, BlinkMacSystemFont, "Segoe UI", Roboto, Oxygen, Ubuntu, Cantarell, "Fira Sans", "Droid Sans", "Helvetica Neue", sans-serif; font-size: 16px; font-style: normal; font-variant-ligatures: normal; font-variant-caps: normal; letter-spacing: normal; orphans: 2; text-align: left; text-indent: 0px; text-transform: none; white-space: normal; widows: 2; word-spacing: 0px; -webkit-text-stroke-width: 0px; background-color: rgb(255, 255, 255); text-decoration-style: initial; text-decoration-color: initial; float: none; display: inline !important;'>&nbsp;</h4> 
K-means Clustering takes an iterative approach to perform the clustering task. The working steps of this algorithm are as follows-
Step 1: Choose the number K of clusters.
Step 2: Select at random K points, the centroids(not necessarily from our dataset).
Step 3: Assign each data point to the closest centroid based on euclidian or manhattan distance. That forms K clusters.
Step 4: Compute and place the new centroid of each cluster.
Step 5:&nbsp;Reassign each data point to the new closest centroid. If any reassignment took place, go to step 4.
It stops creating or optimizing clusters if either the centroids have stabilized meaning no new reassignment of data points takes place or the algorithm reaches the defined number of iterations.
<h5>Choosing The Optimal Number of Clusters</h5>
The value of k is very crucial for optimal outcomes from the algorithm. There are several techniques to choose the optimal value for k including-<ul><li>Cross-Validation, </li><li>Silhouette Method</li><li>G-means Algorithm</li><li>Elbow Method</li></ul>Here we will implement the elbow method to find the optimal value for k.
As the K-means algorithm works by taking the distance between the centroid and data points, we can intuitively understand that the higher number of clusters will reduce the distances among the points. For that, we plot the number of clusters k and the Within Cluster Sum of Squares(WCSS). The plot would look like an elbow, as with an increasing number of clusters after a certain point, the WCSS starts to stabilize and tends to go parallel with the horizontal axis. So we will take that point after which the plot tends to become similar.
&nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp;<img src="/uploads/tutorials/2019/07/23_3_K_means_clustering.png" alt="23_3_K_means_clustering"> 
The Within Cluster Sum of Squares(WCSS) is used to calculate the variance in the data points. The goal of the algorithm is to minimize this value.
<img src="/uploads/tutorials/2019/07/23_2_k_means_clustering.png" alt="23_2_k_means_clustering"> 
<h4>Implementing K-means Clustering in Python</h4>Now, we will implement the above idea in Python using the sklearn library. Let's assume we have a dataset(Mall_Customer.csv) where the details of all customers in a mail are recorded. The features are the genre of the customers(Male or Female), their age, annual income and spending score on a scale of 1 to 100. The data are unlabeled that is there is no output column like in a regression or classification dataset. So, the problem falls in the unsupervised class. Now, our task is to find a number of groups among the customers according to their annual income and spending score. Let's apply K-means clustering and see what happens.<img data-filename="4_K_means_clustering.png" style="width: 529px;" src="/uploads/tutorials/2019/07/23_4_K_means_clustering.png">.You can download the whole dataset form <a href="https://www.dropbox.com/s/s4372co0tkqtof2/Mall_Customers.csv?dl=0" target="_blank">here.</a>First of all, we will import essential libraries. You will get the code in <a href="https://colab.research.google.com/drive/1We5QtM_1M1eGsNQUNpscpEfE5uMPYamx?usp=sharing" target="_blank">Google Colab</a> also.<pre>import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
</pre>
Now, we will import the dataset to our program. Then we will take those features that will effective for our clustering. Here we are interested in the annual income and spending score. So we will take them to our program.<pre>dataset = pd.read_csv('Mall_Customers.csv')
X = dataset.iloc[:, [3, 4]].values</pre>
We need to find the number of cluseter or k. For this we will plot a elbow method graph to find the optimal value for k.<pre># Using the elbow method to find the optimal number of clusters
from sklearn.cluster import KMeans
wcss = []
for i in range(1, 11):
 kmeans = KMeans(n_clusters = i, init = 'k-means++', random_state = 42)
 kmeans.fit(X)
 wcss.append(kmeans.inertia_)
plt.plot(range(1, 11), wcss)
plt.title('The Elbow Method')
plt.xlabel('Number of clusters')
plt.ylabel('WCSS')
plt.show()
</pre>Note:&nbsp;Here, the parameter init is set to k-means++ to avoid the random initialization trap.Let's see the graph&nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp;<img data-filename="6_K-means_clustering (2).png" style="width: 460px;" src="/uploads/tutorials/2019/07/23_6_K-means_clustering_(2).png">From the above graph, we can see that the optimal value for k is 5(the point where the clustering going parallel with the increasing number of clusters).&nbsp;<pre># Fitting K-Means to the dataset
kmeans = KMeans(n_clusters = 5, init = 'k-means++', random_state = 42)
y_kmeans = kmeans.fit_predict(X)
</pre>
 Well, we will come to the coolest part of our algorithm. Now we will visualize the outcomes to see what it has done.
&nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp;<img data-filename="6_K-means_clustering.png" style="width: 441px;" src="/uploads/tutorials/2019/07/23_6_K-means_clustering.png">We can see that the data points are grouped in 5 clusters as we defined in the algorithm. This algorithm is one of the simplest clustering algorithms and has various business uses.<h4>Uses of K-means Clustering</h4>Clustering is widely used in many domains from business to biology. Here are some cool applications of K-means clustering-<ul><li>Market Research Clustering is used to find purchasing patterns among consumers and group them into distinct clusters. The marketer can take different sales strategy according to the groups.</li><li>Website Traffic Analysis Clustering helps to segment the traffic of a website into various classes. This helps to improve the content of a website.</li><li>Grouping Search Result&nbsp; Search engines use cluster analysis to group all the relevant information for a keyword is searched.</li><li>Image Compression&nbsp;In image processing, clustering is used to group similar pixels and make them into groups for compressing the image.</li><li>Gene Segmentation In the field of biology, clustering is useful to find similar genes according to their behavior.</li><li>Anomaly Detection Clustering is widely used to detect fraud using credit card</li><li>Recommendation Engines Clustering is used to find the certain behavioral patterns of users and then the patterns are then used to build recommendation engines</li></ul><h5>Choosing the Distance Metric for Clustering</h5>There are many distance metrics that can be used with clustering algorithms. It depends on the type of data you are using. The default distance metric for sklearn clustering is the Euclidian distance. Here are some points about the distance metrics when to use them-<ul><li>Euclidian Distance: Euclidian distance works well with clusters that have a flat geometrical shape. According to <a href="https://scikit-learn.org/stable/modules/clustering.html" target="_blank">Sklearn documentation,</a> the most used distance metric for flat geometrical clusters is Euclidian distance.</li><li>Manhattan Distance: Manhattan distance is an alternative to Euclidian distance and works somehow similar on flat geometrical clusters.</li><li>Graph Distance: For non-flat geometrical shapes, graph distance is the best. You can apply metrics like k-nearest neighbor graphs to do so.</li><li>Mahalonbish Distance: This distance metric is used in the case of flat geometry and <a href="https://scikit-learn.org/stable/modules/mixture.html#mixture" target="_blank">Gaussian mixture </a>models.</li><li>Correlation Based Distance: This type of distance metrics are often most useful in cases such as gene expression data analysis.</li></ul><h5>What is the Time Complexity of K-means Clustering?</h5>K-means clustering falls in the class of NP-hard problems. So the time complexity is polynomial.In most cases, the worst complexity for K-means clustering is O(n^2 * log(n)) Where n is the number of points.More precisely, the complexity should be expressed as- O(ndk)Where,&nbsp;n=number of data pointsd = dimension of the data&nbsp;k = number of clustersResearch is going on to implement K-means with less time complexity such as <a href="https://ieeexplore.ieee.org/document/7065640" target="_blank">this</a>, where the time complexity is reduced to O(n) using cluster shifting.<h5>Why K-means Clustering is a Non-Deterministic Algorithm?</h5>K-means clustering gets non-deterministic natures due to its random selection of data points as initial centroids. For this randomness, you will get different results on the same instance of data set for different execution. This nature limits the applicability of K-means clustering in areas such as cancer prediction using gene expression data. The result can be misinterpreted when comparing with other models. But some measures can be taken such as <a href="https://pubmed.ncbi.nlm.nih.gov/29100115/" target="_blank">fixing the choice of initial centroid</a> to decrease the randomness and making the model close to deterministic.<h4>Final Words</h4>In this tutorial, I have tried to present and explain all the basic concepts of K-means clustering to you. In summary, the key takeaways are-<ul><li>What K-means clustering is and how it works</li><li>Python implementation of the idea to solve a business problem</li><li>Understanding the nature of the algorithm and choosing the best distance metric</li><li>Learning the uses of K-means clustering</li></ul>Hope the tutorial helped you to understand the concepts.What difficulties you faced or new things discovered when doing K-means clustering?Please let us know in the comments.Happy Machine Learning!

A Simple Explanation of K-means Clustering in Python

Clustering: Clustering is an unsupervised learning algorithm. A cluster refers to groups of aggregated data points because of certain similarities among them. Clustering algorithms group the data points without referring to known or labeled outcomes.
There are commonly two types of clustering algorithms, namely <a href="http://www.aionlinecourse.com/tutorial/machine-learning/clustering" target="_blank">K-means Clustering</a> and Hierarchical Clustering. In this tutorial, we are going to understand and implement Hierarchical Clustering.
Hierarchical Clustering:
This is an unsupervised clustering algorithm that makes clusters of data points in a top-to-bottom or a bottom-up approach. The working principle of Hierarchical clustering can be intuitively understood by a tree-like hierarchy i.e. how different files are organized in sub-folders where the sub-folders are organized in folders. There are two basic distinctions of this algorithm based on their approach.
<ol><li>
 Agglomerative Hierarchical Clustering- follows a bottom-up approach
 </li>
 <li>
 Divisible Hierarchical Clustering- follows a top to bottom approach
 </li>
</ol>In this tutorial, we will focus on Agglomerative Hierarchical Clustering.
Agglomerative Hierarchical Clustering:
In this technique, Initially, each data point is taken as an individual cluster. Then the similar clusters are merged together at each iteration based on their proximity with each other. The algorithms run until one cluster or a defined number of clusters are found.
How Does The Algorithm work?
The working steps of the algorithm are as follows
Step 1: Make each data point a single-point cluster. That forms N clusters.
Step 2: Take the two closest data points and make them one cluster. That forms N-1 clusters.
Step 3: Take the two closest clusters and make them one cluster. That forms N-2 clusters
Step 4: Repeat Step 3 until there is only one cluster.
Let's apply these steps one by one clustering data points
We take six data points here.
&nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp;&nbsp;<img src="/uploads/tutorials/2019/07/25_2_Hierarchical_clustering.png" alt="25_2_Hierarchical_clustering"> 
Step 1: Make each data point an individual cluster. That makes six clusters here
&nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp;<img src="/uploads/tutorials/2019/07/25_1_HIerarchical_clustering.png" alt="25_1_HIerarchical_clustering"> 
 
Step 2: Make two closest data points and make them one cluster. That forms 5 clusters.
 
&nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp;<img src="/uploads/tutorials/2019/07/25_3_hierarchical_clustering.png" alt="25_3_hierarchical_clustering">
 
Step 3: Take the two closest clusters and make them one cluster. That forms 4 clusters.
 
&nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp;<img src="/uploads/tutorials/2019/07/25_4_Hierarchical_clustering.png" alt="25_4_Hierarchical_clustering"> 
 
Step 4: Repeat step 3 until there is only one cluster.
 
&nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp;&nbsp;<img src="/uploads/tutorials/2019/07/25_5_hierarchical_clustering.jpg" alt="25_5_hierarchical_clustering"> 
 
 
In K-means clustering, we use the elbow method for selecting the number of clusters. For Hierarchical Clustering, we use a dendrogram to find the number of clusters.&nbsp;
Dendrogram: A Dendrogram is a tree-like diagram that records the sequences of merges or splits that occurred in the various steps of Hierarchical clustering. It's very helpful to intuitively understand the clustering process and find the number of clusters.
 
<img src="/uploads/tutorials/2019/07/25_7_Hierarchical_clustering.png" alt="25_7_Hierarchical_clustering"> 
 
It keeps track of the merges of the clusters in a sequential order like above i.e. the P2 and P3 clusters are merged first, then P5 and P6 and so on. What does is that it calculates the dissimilarity or distance between the clusters and represents it with the vertical lines. The longer the distance the longer the verticals will be.
 
To find the number of clusters k, we set a threshold value on the vertical axis. Then we count those vertical lines which are the longest and do not intersect with other vertical lines. This count is taken as the number of clusters.
 
&nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp;&nbsp;<img src="/uploads/tutorials/2019/07/25_2019-07-24_(3)_LI.jpg" alt="25_2019-07-24_(3)_LI"> 
 
HC in Python:&nbsp;Now, we will implement this algorithm in Python. First, we will set the working directory. Here we are using the&nbsp;Mall_Customers.csv dataset. Let's have a glimpse of that dataset.&nbsp;&nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp;<img data-filename="23_4_Hierarchical_clustering.png" style="width: 529px;" src="/uploads/tutorials/2019/07/25_23_4_Hierarchical_clustering.png">The dataset contains the data of some customers in a mall. Here we do not have any certain outcome or labeled output. So, we will implement Hierarchical Clustering to find some useful classes from this dataset.You can download the whole dataset from <a href="https://www.dropbox.com/s/s4372co0tkqtof2/Mall_Customers.csv?dl=0" target="_blank">here.</a>First of all, we will import essential libraries. You will get the code in <a href="https://colab.research.google.com/drive/1WD4JmQtInqNyo75Xxpvw-aiY8VtMuhTu?usp=sharing" target="_blank">Google Colab</a> also.<pre>import numpy as np
import matplotlib.pyplot as plt
import pandas as pd</pre>Now, we will import the dataset. From the dataset, we will take the Annual Income and Spending Score in the feature matrix.<pre style="font-size: 14px;">dataset = pd.read_csv('Mall_Customers.csv')
X = dataset.iloc[:, [3, 4]].values</pre>We need to find the number of clusters. For this, we will generate a dendrogram.<pre># Using the dendrogram to find the optimal number of clusters
import scipy.cluster.hierarchy as sch
dendrogram = sch.dendrogram(sch.linkage(X, method = 'ward'))
plt.title('Dendrogram')
plt.xlabel('Customers')
plt.ylabel('Euclidean distances')
plt.show()
</pre>
 &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp;&nbsp;<img data-filename="8_Hierarchical_clustering.png" style="width: 445px;" src="/uploads/tutorials/2019/07/25_8_Hierarchical_clustering.png"> We set the threshold at 200(euclidian distance) and get 5 vertical lines that do not intersect with other lines. So the number of clusters will be 5.Now, we will fit the Agglomerative HC into our dataset.<pre># Fitting Hierarchical Clustering to the dataset
from sklearn.cluster import AgglomerativeClustering
hc = AgglomerativeClustering(n_clusters = 5, affinity = 'euclidean', linkage = 'ward')
y_hc = hc.fit_predict(X)</pre> We have come to the final part. Let's visualize what our model has done!<pre># Visualising the clusters
plt.scatter(X[y_hc == 0, 0], X[y_hc == 0, 1], s = 100, c = 'red', label = 'Cluster 1')
plt.scatter(X[y_hc == 1, 0], X[y_hc == 1, 1], s = 100, c = 'blue', label = 'Cluster 2')
plt.scatter(X[y_hc == 2, 0], X[y_hc == 2, 1], s = 100, c = 'green', label = 'Cluster 3')
plt.scatter(X[y_hc == 3, 0], X[y_hc == 3, 1], s = 100, c = 'cyan', label = 'Cluster 4')
plt.scatter(X[y_hc == 4, 0], X[y_hc == 4, 1], s = 100, c = 'magenta', label = 'Cluster 5')
plt.title('Clusters of customers')
plt.xlabel('Annual Income (k$)')
plt.ylabel('Spending Score (1-100)')
plt.legend()
plt.show()</pre>
&nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp;&nbsp;<img data-filename="9_hierarchical_clustering.png" style="width: 444px;" src="/uploads/tutorials/2019/07/25_9_hierarchical_clustering.png"> 
Hierarchical clustering performs well in a small set of data. For a large dataset, this algorithm does not fit well. You should use <a href="http://www.aionlinecourse.com/tutorial/machine-learning/clustering" target="_blank">K-means clustering </a>instead.

Hierarchical Clustering

Association Rule Learning | Apriori

Eclat Intuition: Today, we are talking about the Eclat model. It is similar to the&nbsp;Apriori&nbsp;algorithm. Here, we actually talking about the rules. Because the cloud model is different from the a priori model. In Eclat intuition, the cloud model is just like in the&nbsp;Apriori&nbsp;model we have the support vector. But we do not have confidence and lift factors. We are only looking for support. It much faster and the steps involved are set minimum support so we want to set up a support level.<img data-filename="eclat_1.png" style="width: 773px;" src="/uploads/tutorials/2018/09/21_eclat_1.png"> 

There are several steps:
 
Step 1: Set a minimum support.
 
Step 2: Take all the subsets in a transaction having higher support than minimum support.
 
Step 3: Sort these subsets by decreasing support.

Eclat Intuition

Reinforcement Learning is a branch of Machine Learning, also called Online Learning. It is used to solve interacting problems where the data observed up to time t is considered to decide which action to take at time t + 1. It is also used for Artificial Intelligence when training machines to perform tasks such as walking. Desired outcomes provide the AI with reward, undesired with punishment. Machines learn through trial and error.
Reinforcement Learning is learning how to act in order to maximize a numerical reward.
In this part, you will understand and learn how to implement the following Reinforcement Learning models:
<ol><li>
 Upper Confidence Bound (UCB)
 </li>
 <li>
 Thompson Sampling<img data-filename="reinforcement_learning_aionlinecourse_1.png" style="width: 558px;" src="/uploads/tutorials/2023/08/15_reinforcement_learning_aionlinecourse_1.png"><img data-filename="reinforcement_learning_aionlinecourse_2.png" style="width: 554px;" src="/uploads/tutorials/2023/08/15_reinforcement_learning_aionlinecourse_2.png"> 
 </li>
</ol>

Reinforcement Learning in Machine Learning

Upper Confidence Bound (UCB) Algorithm: Solving the Multi-Armed Bandit Problem

In this article, we will talk about the Thompson Sampling Algorithm for solving the multi-armed bandit problem and implement the algorithm in Python.
Thompson Sampling Algorithm: Thompson Sampling is one of the oldest heuristics to solve the Multi-Armed Bandit problem. This is a probabilistic algorithm based on Bayesian ideas. It is called sampling because it picks random samples from a probability distribution for each arm. This could be defined as a Beta Bernoulli sampler. Though Thompson sampling can be generalized to sample from any arbitrary distributions. But the Beta Bernoulli version of Thompson sampling is more intuitive and is actually the best option for many problems in practice. In this tutorial, we will use the Beta Benouli sampler.
 
Algorithm Comparison: Upper Confidence Bound vs. Thompson Sampling: There is a significant difference between UCB and Thompson sampling. Firstly UCB is a deterministic algorithm whereas Thompson sampling is a probabilistic algorithm. In UCB you must incorporate the value at every round, you cannot proceed to the next round without adjusting the value. In Thompson, you can accommodate delayed feedback. This means you can update the dataset for your multi-armed bandit problem in a batch manner, that will save your additional computing resource or cost of updating the dataset each time. This is the main advantage of Thompson sampling over UCB.
 
Recently, it has generated significant interest after several studies demonstrated it to have better empirical performance compared to the UCB algorithm.
How this Algorithm Works?
Let's say we have three multi-armed bandits with the following distributions
&nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp;<img src="/uploads/tutorials/2018/09/21_thm_sam_2.png" alt="21_thm_sam_2" style="width: 100%;"> 
In the above distribution, our expected value can anywhere in the distribution. Now, this algorithm will choose samples from the above distribution using Bayesian Inference rules. First, it will run some trial rounds before doing the actual computation.
&nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp;<img src="/uploads/tutorials/2019/06/14_2_Thompson_Sampling.png" alt="14_2_Thompson_Sampling" style="width: 100%;"> 
Now, it will pick the samples from each of the distributions that have the highest value of the distribution. This will make an imaginary set of bandits. That means that this algorithm actually makes an auxiliary mechanism to solve the problem, that is, it will not create the machines at every round rather it will create the possible ways these machines could be recreated. With each trial, each takes a sample that has the highest distribution. And with each trial, the distribution will be changed. The distribution will get narrower as we have some information. After a huge number of rounds, we will get the narrowest distribution which we will take as the final outcome.
&nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp;<img src="/uploads/tutorials/2019/06/14_3_Thompson_Sampling.png" alt="14_3_Thompson_Sampling" style="width: 100%;"> 
Now let's look at the steps of the algorithm.
&nbsp;
Let's implement this algorithm for our own version of a multi-armed bandit problem. Here we will take a dataset of online advertising campaigns where an ad has 10 different versions. Now our task is to find the best ad using the Thompson sampling algorithm.
&nbsp;
Let's look at the steps we need in Thompson sampling:
&nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp;&nbsp;<img src="/uploads/tutorials/2019/06/14_5_Thompson_Sampling.png" alt="14_5_Thompson_Sampling" style="width: 100%;">
 
At the first step, the total number of rewards(either 0 or 1) is counted.
To understand the second step, we need to look at the Bayesian inference rules-
&nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp;&nbsp;<img src="/uploads/tutorials/2019/06/14_6_Thompson_Sampling.png" alt="14_6_Thompson_Sampling" style="width: 100%;"> For step 2, we have two assumptions, first, we say that each ad i gets a reward from a Bernoulli distribution which is the probability of success. You can picture this parameter by showing this ad to a million users and the parameter will be interpreted as the number of times the outcomes were ones divided by the number of ads. Basically, it is the probability of getting ones. The second assumption is that we have a uniform distribution which is a prior distribution, then we have the posterior distribution from the Bayes rule that is the probability of success given the rewards after the round n. By doing this Bayes rule we get the beta distribution here. In Thompson sampling, these random draws mean nothing but the probability of success, because the maximum of these random draws approximating the highest probability of success. And this is the idea behind Thompson sampling. By taking the highest of these draws we are maximizing the probability of success for each of the 10 ads. And this highest probability corresponds to each ad at every round. &nbsp;After performing the algorithm we will take the highest ad having the highest probability of success.
Thompson sampling in Python: First of all, we need to import essential libraries. You will get the code in <a href="https://colab.research.google.com/drive/1jn3VIeTYREBYU0W8vi1Qj3ddUAIDVm58?usp=sharing" target="_blank">Google Colab</a> also.<pre>import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
</pre>Then we will import our dataset (Ads_CTR_Optimisation.csv)
You can download the dataset from <a href="https://www.dropbox.com/s/ovnpvh8y50qain5/Ads_CTR_Optimisation.csv?dl=0">here.</a><pre># Importing the dataset 
dataset = pd.read_csv('Ads_CTR_Optimisation.csv')
</pre>
Now, let's implement the Thompson Sampling code<pre class="dropdown-item"><pre class="dropdown-item"># Implementing Thompson Sampling</pre><pre class="dropdown-item">import random</pre><pre class="dropdown-item">N = 10000</pre><pre class="dropdown-item">d = 10</pre><pre class="dropdown-item">ads_selected = []</pre><pre class="dropdown-item">numbers_of_rewards_1 = [0] * d</pre><pre class="dropdown-item">numbers_of_rewards_0 = [0] * d</pre><pre class="dropdown-item">total_reward = 0</pre><pre class="dropdown-item">for n in range(0, N):</pre><pre class="dropdown-item">&nbsp; &nbsp; ad = 0</pre><pre class="dropdown-item">&nbsp; &nbsp; max_random = 0</pre><pre class="dropdown-item">&nbsp; &nbsp; for i in range(0, d):</pre><pre class="dropdown-item">&nbsp; &nbsp; &nbsp; &nbsp; random_beta = random.betavariate(numbers_of_rewards_1[i] + 1, numbers_of_rewards_0[i] + 1)</pre><pre class="dropdown-item">&nbsp; &nbsp; &nbsp; &nbsp; if random_beta &gt; max_random:</pre><pre class="dropdown-item">&nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; max_random = random_beta</pre><pre class="dropdown-item">&nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; ad = i</pre><pre class="dropdown-item">&nbsp; &nbsp; ads_selected.append(ad)</pre><pre class="dropdown-item">&nbsp; &nbsp; reward = dataset.values[n, ad]</pre><pre class="dropdown-item">&nbsp; &nbsp; if reward == 1:</pre><pre class="dropdown-item">&nbsp; &nbsp; &nbsp; &nbsp; numbers_of_rewards_1[ad] = numbers_of_rewards_1[ad] + 1</pre><pre class="dropdown-item">&nbsp; &nbsp; else:</pre><pre class="dropdown-item">&nbsp; &nbsp; &nbsp; &nbsp; numbers_of_rewards_0[ad] = numbers_of_rewards_0[ad] + 1</pre><pre class="dropdown-item">&nbsp; &nbsp; total_reward = total_reward + reward</pre></pre>Now, we have come to the final part of our program. Let's visualize what we got-<pre>plt.hist(ads_selected)
plt.title('Histogram of ads selections')
plt.xlabel('Ads')
plt.ylabel('Number of times each ad was selected')
plt.show()
</pre>&nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp;&nbsp;<img src="/uploads/tutorials/2018/09/21_thm_sam_5.png" alt="21_thm_sam_5" style="width: 100%;"> 
 
 
In the above histogram, you can see that ad version five has the highest probability of success. So we will take the fifth version of the ad as output. If you compare this result with our previous <a href="http://www.aionlinecourse.com/tutorial/machine-learning/upper-confidence-bound-%28ucb%29">Upper Confidence Bound</a>&nbsp;result, you will see a clear difference. Though the UCB algorithm found the same ad version as of Thompson sampling, the Thompson sampling showed better empirical evidence than UCB in practice.

Thompson Sampling Intuition

In this article, we are going to learn and implement an Artificial Neural Network(ANN) in Python.
Artificial Neural Network: An artificial neural network (ANN), usually called a neural network" (NN) is a mathematical model or computational model that tries to simulate the structure and functional aspects of biological neural networks. It consists of an interconnected group of artificial neurons and processes information using a&nbsp; connectionist approach to computation.
To get a clear idea, let's take a look at a biological neuron.
&nbsp;<img src="/uploads/tutorials/2023/09/human_neuron_aionlinecourse.com">
A human neuron has three parts- the main body, the axon, and the dendrites. Though one neuron itself does not have any significance, when millions or probably billions of neurons work together, they can process a task like reading and understanding this article.&nbsp;
Well, you can think of an artificial neuron as a simulation of a human neuron. It tries to mimic the works of a human neuron using mathematics and machine learning algorithms. Here is also, as a biological neuron, a single AN can not do any significant task. But when we connect a number of neurons in layers, they together can do some tasks like classification or regression.
<img src="/uploads/tutorials/2023/09/ann_example_2_aionlinecourse.png">&nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp;&nbsp;
Here you can see a simplified illustration of an artificial neuron. It takes inputs from some neurons i.e. x1, x2, xm, processes them using some mathematical functions called activation functions and produces an output. ANN has much more complex structures. It also includes some hidden layers and other structures.
Activation Functions: An activation function directs the output of a neuron or node, which means after receiving a set of inputs, it chooses what will be the output of that neuron. Depending on the kind of activation function, the output of a neuron varies. There are various types of activation functions. But these four are prominent ones.<ul><li>Threshold Function: This is the most basic type of activation function. It simply outputs a yes/no type of value. When the weighted sum is(the sum of weighted input from the input layers) less than zero, it simply provides 0, and when the weighted sum is greater or equals to zero, it provides</li><li>Sigmoid Function: This is one of the most used activation functions. It provides a continuous output. If the input value is less than zero its output will be zero. For a value zero or greater than zero it provides a continuous output value ranges between zero and one. It is a useful function for tasks like regressions. It is usually used in the output node.</li><li>Rectifier Function: It is one of the most popular activation functions. It provides a zero for a negative value and gradually increases to one for a positive value. It is widely used in the input layer nodes.</li><li>Hyperbolic tangent function: It provides output for both negative and positive input values.</li></ul><h4>How Does the Neural Network Work?</h4>
When we connect a number of artificial neurons, that forms a neural network. Then the network can carry out some tasks like classification and regression. To understand the whole idea, let's take an example, assume that we need to find the price of an apartment in a particular area, where the input parameters are the area of the apartment, number of bedrooms, how far it is from the city, and the age of the apartment. Now let's build an ANN model that will predict the price of a particular apartment using this set of input parameters. We are not going into the details, but assume that in the hidden layer we are using an activation function i.e. Rectifier function that calculates the weighted input and pass a value to the output layer where we are using another activation function i.e. Sigmoid function, that upon the input from the hidden layer, calculates the probable value of that apartment. Here we have shown a simplified feedforward network, you may need to use more complex models for other problems.
<img src="/uploads/tutorials/2023/09/ann_aionlinecourse.png"> 
<h4>How do Neural Networks Learn?</h4>
Though the idea of learning neural networks is a bit complex, we can simplify the concept. In a simple sense, we feed in inputs to the input layer nodes(individual neurons), which are connected to some hidden layer nodes. The inputs are processed and fed to the output layer. Then we compare the predicted value with the actual value using a cost function. In ML,&nbsp; a cost function is used to measure how good or bad a model is performing. Here we take a cost function, C which is the squared average difference between the predicted and actual outcomes.<img src="/uploads/tutorials/2023/09/ann_example_aionlinecourse.png"> 
Then we update the weights in the input layer based on the cost function output. This update is performed by using a gradient descent function. This type of network is called a backpropagation network. Because we are providing the input and updating the weights from the output iteratively.&nbsp;
After some iterations (until a satisfactory outcome), we assume that the model has learned successfully.
<h5>Gradient Descent Function</h5> Gradient descent is an optimization algorithm for updating the weights to the input layer nodes after the comparison done by the cost function. It uses a first-order differential equation that tries to minimize the cost function. That means it tries to find the lowest error value.<img src="/uploads/tutorials/2023/09/gradient_descent_aionlinecourse.png"> 
There are various types of gradient descent functions. Among them, the Batch gradient descent function (shown above) and Stochastic gradient descent function are most commonly used.
The stochastic gradient descent function is more optimized than the Batch gradient function as it can avoid the local minimum. Local minimum happens when the gradient function finds a minimum error value that seems fine initially. But if the function could go further it would find the best minimum error value.In this article, we will use the stochastic gradient descent function.&nbsp;
Let's understand the steps required to train a model with Stochastic gradient Descent&nbsp;
STEP 1: Randomly initialize the weights to small numbers close to 0 (but not 0).&nbsp;
STEP 2: Input the first observation of your dataset in the input layer, each feature in one input node.&nbsp;
STEP 3: Forward-propagation: From left to right, the neurons are activated in a way that the impact of each neuron's activation is limited by the weights. Propagate the activations until getting the predicted result y.&nbsp;
STEP 4: Compare the predicted result to the actual result. Measure the generated error.&nbsp;
STEP 5: Back-propagation: from right to left, the error is back-propagated. Update the weights according to how much they are responsible for the error. The learning rate is decided by how much we update the weights.&nbsp;
STEP 6: Repeat Steps 1 to 5 and update the weights after each observation (Reinforcement Learning). Or: Repeat Steps 1 to 5 but update the weights only after a batch of observations (Batch Learning).&nbsp;
STEP 7: When the whole training set passes through the ANN, that makes an epoch. Redo more epochs.
ANN in Python: In this tutorial, we are going to implement an artificial neural network in Python.&nbsp; We have a dataset of a bank containing the transaction data of customers. Let's have a look at the dataset-<img src="/uploads/tutorials/2023/09/ann_dataset_aionlinecourse.png"> You can download the whole dataset from <a href="https://web.archive.org/web/20220704210114/https://www.dropbox.com/s/oklux19m1i821dk/Churn_Modelling.csv?dl=0" target="_blank">here.</a>The dataset contains a number of different features. Now, using these features of the dataset, our task is to classify whether a customer stays or departs from the bank. So this is a classification problem.For building neural networks we need libraries and modules like Keras, Theona, and TensorFlow. Ensure that you have properly installed them in your Anaconda environment. You can find the guidelines for installing these<a href="https://web.archive.org/web/20220704210114/https://keras.io/#installation" target="_blank"> here.</a>&nbsp;You will get the code in <a href="https://colab.research.google.com/drive/16gQbRLKsfWZXWItDmz05frxV9q_HF-ER?usp=sharing" target="_blank">Google Colab</a> also.First of all, we will import some essential libraries.&nbsp;
<pre># Importing the libraries
import numpy as np
import pandas as pd
import tensorflow as tf</pre>

In the dataset, the last column Exited&nbsp;represents the state of a customer(stays or leaves) and is the only dependent variable. So we will take this column in the dependent variable vector. The rest of the columns are independent, so we will take all except the first three columns into the feature matrix.
<pre># Importing the dataset
dataset = pd.read_csv('Churn_Modelling.csv')
X = dataset.iloc[:, 3:-1].values
y = dataset.iloc[:, -1].values</pre>Here some of the features are categorical variables. So we will encode them.
<pre># Encoding categorical data
# Label Encoding the "Gender" column
from sklearn.preprocessing import LabelEncoder
le = LabelEncoder()
X[:, 2] = le.fit_transform(X[:, 2])

# One Hot Encoding the "Geography" column
from sklearn.compose import ColumnTransformer
from sklearn.preprocessing import OneHotEncoder
ct = ColumnTransformer(transformers=[('encoder', OneHotEncoder(), [1])], remainder='passthrough')
X = np.array(ct.fit_transform(X))</pre>
Now we split the dataset into training and test sets.
<pre># Splitting the dataset into the Training set and Test set
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.2, random_state = 0)
</pre><div>We need to scale our dataset. For this, we will use the StandardScaler library. </div>
<pre># Feature Scaling
from sklearn.preprocessing import StandardScaler
sc = StandardScaler()
X_train = sc.fit_transform(X_train)
X_test = sc.transform(X_test)</pre>Now, we have come to the main part of our program. We will build a neural network using the Keras library. 
<pre># Importing the Keras libraries and packages
import keras
from keras.models import Sequential
from keras.layers import Dense</pre>
We will initialize the ANN using the Sequential class from Keras.
<pre># Initialising the ANN
ann = tf.keras.models.Sequential()</pre>
Now, we will add&nbsp;the hidden layer. The dataset contains eleven independent variables. It is a rule of thumb that we take half of the dependent variable in the hidden layer. So the&nbsp;units&nbsp;parameter is set to 6. Here we used the rectifier functions as the activation function.
<pre># Adding the input layer and the first hidden layer
ann.add(tf.keras.layers.Dense(units=6, activation='relu'))</pre>
&nbsp;We can add more than one hidden layer to our network.
<pre># Adding the second hidden layer
ann.add(tf.keras.layers.Dense(units=6, activation='relu'))</pre>
Now, we will add the output layer. Here, we have only one dependent variable. So our output layer only contains one node. We used the sigmoid function as the activation function.<pre># Adding the output layer
ann.add(tf.keras.layers.Dense(units=1, activation='sigmoid'))</pre>
&nbsp;Let's compile the whole ANN before starting to run. Here we use the stochastic gradient descent function as the optimizer. adam is one of the most used stochastic gradient descent functions. We choose binary_crossentropy as the loss function as this is a binary classification problem.
<pre># Compiling the ANN
ann.compile(optimizer = 'adam', loss = 'binary_crossentropy', metrics = ['accuracy'])</pre>It's time to fit the classifier algorithm into our dataset. we take the number of iteration, nb_epoch to 100 which means the whole network will run a hundred times.
<pre># Fitting the ANN to the Training set
ann.fit(X_train, y_train, batch_size = 32, epochs = 100)
</pre><div>Now, we will predict the outcome of the ANN.</div>
<pre>y_pred = ann.predict(X_test)
y_pred = (y_pred &gt; 0.5)
print(np.concatenate((y_pred.reshape(len(y_pred),1), y_test.reshape(len(y_test),1)),1))</pre>

Let's see how good our model is for making the prediction.
<pre>from sklearn.metrics import confusion_matrix, accuracy_score
cm = confusion_matrix(y_test, y_pred)
ac = accuracy_score(y_test, y_pred)
print(cm)
print(ac)</pre>

From the above confusion matrix, we can see the accuracy of the model is 84%.

Artificial Neural Networks

Natural Language Processing: Natural language processing (NLP) is a field of artificial intelligence concerned with the interactions between computers and human(natural) language.
In a simple sense, Natural language Processing is applying machine learning to text and language to teach computers to understand what is said in spoken and written words. The main focus of NLP is to read, decipher, understand and make sense of the human language in a manner that is useful.&nbsp;
Examples of NLP in Real Life: You will find a lot of applications of NLP in your life. Here we name a few-
<ul><li>
 Translating one language to another i.e. Google Translator
 </li>
 <li>
 Checking grammatical errors i.e. Microsoft word or Grammarly applies NLP to check and correct grammatical errors.
 </li>
 <li>
 Sentiment analysis that is identifying the mood or subjective opinions of a text
 </li>
 <li>
 Summarizing a text or article
 </li>
 <li>
 Predicting the genre of books
 </li>
 <li>
 Speech recognition which is used in virtual assistants such as Apple Siri, Google Assistant, and Amazon Alexa
 </li>
 <li>
 Question answering
 </li>
</ul>How NLP Works?
Most NLP algorithms are classification models, and they include Logistic Regression, Naive Bayes,&nbsp; CART which is a model based on decision trees, Maximum Entropy and other classification algorithms to predict the outcome.
The working procedure of NLP can be divided into three major steps:
Step 1: Preprocessing of text that includes Cleaning the data, Tokenizing, Stemming, Parts of Speech(POS) Tagging, Lemmatization, Named Entity Recognition (NER)
Step 2: This step is for vectorizing data, that is encoding text into integer i.e. numeric form to create a feature vector.
Step 3: The final step is to fit a suitable classification algorithm to the dataset and make the predictions.
We can implement all these steps using NLP libraries. Some of the popular NLP libraries are-
<ul><li>
 Natural Language Toolkit-NLTK
 </li>
 <li>
 SpaCy
 </li>
 <li>
 Stanford NLP
 </li>
 <li>
 OpenNLP
 </li>
</ul>In this article, we are going to implement all these steps using the NLTK library and classification algorithm. From this part, you will learn how to-
<ul><li>
 Clean texts to prepare them for the Machine Learning models,
 </li>
 <li>
 Create a Bag of Words model,
 </li>
 <li>
 Apply Machine Learning models onto this Bag of Worlds model. 
 </li>
</ul>Natural Language Processing in Python: Now, we will perform the steps of NLP in Python. For this task, we are going to use Restaurant_Reviews.tsv dataset. The dataset contains 1000 reviews from customers. These reviews are identified with values 0 and 1 whether they are positive or negative. 0 means the review is positive and 1 means the review is positive. Let's have a glimpse of that dataset.
<img src="/uploads/tutorials/2019/08/02_1_NLP.png" alt="02_1_NLP">
This dataset looks different than other datasets as it is in tsv(tab-separated value) format. For NLP task we can not use csv(comma-separated value) files. This is because of the strings may contain commas, which will confuse our model.You can download the whole dataset from <a href="https://www.dropbox.com/s/xnbu67gu78l2zyk/Restaurant_Reviews.tsv?dl=0" target="_blank">here.</a>
It contains two columns namely&nbsp;Review&nbsp;and Liked. They are separated by a tab.&nbsp;Now our task is to preprocess this data. Then we will implement any of the classification algorithms to classify the reviews whether it is positive or negative.
First of all, we will import some essential libraries. You will get the code in <a href="https://colab.research.google.com/drive/1cdOYLsO8Vujg_kKpDBbb21Gx9BPoHLzZ?usp=sharing" target="_blank">Google Colab</a> also.<pre># Importing the libraries 
import numpy as np 
import matplotlib.pyplot as plt 
import pandas as pd</pre>
Now we will import the dataset.<pre># Importing the dataset
dataset = pd.read_csv('Restaurant_Reviews.tsv', delimiter = '\t', quoting = 3)</pre>As our dataset is in tsv format, we need to clarify that in the delimiter parameter. The reviews contain double quotes, which may cause confusion to the model. So we set the quoting parameter to 3 to avoid this problem.Now, we will clean the texts using the NLTK&nbsp;library from Python. The texts contain a lot of useless words which have no impact on the characteristic of the review, we need to get rid of those words like wow, place, texture, etc. Then we need to perform stemming that is we will take the root of a word like loved, loving, lovely, etc. all can be replaced by the same word love. The texts also contain some common words like was, that, this, it, is, etc. which are known as stopwords and have no use at all. So we will remove those words using the stopwords package from the NLTK&nbsp;library. We only consider the English words and also take all the words into lowercase.&nbsp;
<pre># Cleaning the texts
import re
import nltk
nltk.download('stopwords')
from nltk.corpus import stopwords
from nltk.stem.porter import PorterStemmer
corpus = []
for i in range(0, 1000):
 review = re.sub('[^a-zA-Z]', ' ', dataset['Review'][i])
 review = review.lower()
 review = review.split()
 ps = PorterStemmer()
 review = [ps.stem(word) for word in review if not word in set(stopwords.words('english'))]
 review = ' '.join(review)
 corpus.append(review)
</pre><div>&nbsp;We proceed to the most important part of NLP, the creation of the bag of words model. A bag of words is a multiset of words that will help us to analyze the different reviews and classify them.</div><div> </div><pre># Creating the Bag of Words model
from sklearn.feature_extraction.text import CountVectorizer
cv = CountVectorizer(max_features = 1500)
X = cv.fit_transform(corpus).toarray()
y = dataset.iloc[:, 1].values</pre>After doing all these steps, the corpus will now look like this-&nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp;<img data-filename="2_NLP.png" style="width: 647px;" src="/uploads/tutorials/2019/08/02_2_NLP.png"> We have completed preprocessing the texts and creating the bag of words model. Now, we split this preprocessed dataset into training and test sets.&nbsp;<pre># Splitting the dataset into the Training set and Test set
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.20, random_state = 0)</pre> Let's fit a classification algorithm into our training set. Here we will use Naive Bayes which is one of the most popular and most effective classification algorithms for NLP. <pre># Fitting Naive Bayes to the Training set
from sklearn.naive_bayes import GaussianNB
classifier = GaussianNB()
classifier.fit(X_train, y_train) </pre>Now, we will perform a prediction on the test set.<pre style="font-size: 14px;"># Predicting the Test set results
y_pred = classifier.predict(X_test)
</pre>&nbsp;Let's see how good is our model in performing predictions using the confusion matrix.<pre style="font-size: 14px;"># Making the Confusion Matrix
from sklearn.metrics import confusion_matrix
cm = confusion_matrix(y_test, y_pred)</pre> &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp;&nbsp;<img data-filename="3_NLP.png" style="width: 214px;" src="/uploads/tutorials/2019/08/02_3_NLP.png"> 
From the above confusion matrix, we can see that the accuracy of our model is 73%.

Natural Language Processing

Deep Learning: Deep Learning is an artificial intelligence function that imitates the workings of the human brain in processing data and creating patterns for use in decision making. Deep learning is a subset of machine learning in Artificial Intelligence (AI) that has networks capable of learning unsupervised from data that is unstructured or unlabeled. Deep Learning is the most exciting and powerful branch of Machine Learning.
 
Deep Learning models can be used for a variety of complex tasks:
<ul><li>
 Artificial Neural Networks for Regression and Classification
 </li>
 <li>
 Convolutional Neural Networks for Computer Vision
 </li>
 <li>
 Recurrent Neural Networks for Time Series Analysis
 </li>
 <li>
 Self Organizing Maps for Feature Extraction
 </li>
 <li>
 Deep Boltzmann Machines for Recommendation Systems
 </li>
 <li>
 AutoEncoders for Recommendation Systems
 </li>
</ul>In this part, you will understand and learn how to implement the following Deep Learning models:
<ol><li>
 Artificial Neural Networks for a Business Problem
 </li>
 <li>
 Convolutional Neural Networks for a Computer Vision task
 </li>
</ol>

Deep Learning

Principal Component Analysis (PCA):&nbsp;Principle Component Analysis or PCA is a popular dimensionality reduction technique that reduces the number of features or independent variables by extracting those features with the highest variance. That means it finds the correlation between the independent variables and calculates their variance, then it selects those features that have the highest variance.
If the dataset contains n variables, the PCA will extract m&lt;=n number of independent variables which explains the most variance of the dataset. It is an unsupervised algorithm as it can extract features regardless of the dependent variable.
PCA in Python:&nbsp;PCA is a very simple and popular algorithm in practice. In this tutorial, we will implement this algorithm alongside with a<a href="http://www.aionlinecourse.com/tutorial/machine-learning/logistic-regression">&nbsp;Logistic Regression</a>&nbsp;algorithm. For this task, we will use the famous "Wine.csv"&nbsp;dataset from the UCI machine learning repository. Our version of the dataset contains thirteen independent variables that represent various aspects of wines and one dependent variable that represents the three types of buyers of the wine based on specific features. Now, we will implement PCA to reduce the number of independent variables to a defined value(i.e. two).
You can download the whole dataset from&nbsp;<a href="https://www.dropbox.com/s/8139t6qk69wt10d/Wine.csv?dl=0">here.</a>&nbsp;You will get the full code in <a href="https://colab.research.google.com/drive/1s6fHY4tz0yFMDOE9P4McUsefaKIWtIux?usp=sharing" target="_blank">Google Colab</a> also.
First of all, we import essential libraries.&nbsp;
<pre>#Importing the libraries import numpy as np import matplotlib.pyplot as plt import pandas as pd</pre>



Now, let's import the dataset and make a feature matrix X and dependent variable y 
<pre>#Importing the dataset dataset = pd.read_csv('Wine.csv') X = dataset.iloc[:, 0:13].values y = dataset.iloc[:, 13].values</pre>



Then we will split the dataset and apply feature scaling.
<pre># Splitting the dataset into the Training set and Test set from sklearn.model_selection import train_test_split X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.2, random_state = 0) &nbsp; # Feature Scaling from sklearn.preprocessing import StandardScaler sc = StandardScaler() X_train = sc.fit_transform(X_train) X_test = sc.transform(X_test) &nbsp;</pre>









Now, we have come to the most important part of the tutorial. Let's implement the PCA algorithm into our dataset.
<pre># Applying PCA from sklearn.decomposition import PCA pca = PCA(n_components = 2) X_train = pca.fit_transform(X_train) X_test = pca.transform(X_test) explained_variance = pca.explained_variance_ratio_</pre>





Here, the parameter&nbsp;n_components&nbsp;&nbsp;represents the number of independent variables we want in our datasets(here we take 2). The algorithm will take those two variables with the highest variance. You can see their variance from the&nbsp;explained_variannce&nbsp;vector.
Now we will fit logistic regression to our dataset and predict the result.
<pre>#Fitting Logistic Regression to the Training set from sklearn.linear_model import LogisticRegression classifier = LogisticRegression(random_state = 0) classifier.fit(X_train, y_train) &nbsp; #Predicting the Test set results y_pred = classifier.predict(X_test)</pre>






 
Let's see how good our model is for making predictions using the confusion matrix.
<pre># Making the Confusion Matrix from sklearn.metrics import confusion_matrix cm = confusion_matrix(y_test, y_pred)</pre>
The confusion matrix will look like following


&nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp;<img data-filename="1_PCA.png" style="width: 317px;" src="/uploads/tutorials/2019/08/05_1_PCA.png">
&nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp;&nbsp;
From the above matrix, we can calculate the accuracy of the model and that comes out to be 97%, quite impressive!
Now, let's visualize both our training and test sets.
<pre># Visualising the Training set results from matplotlib.colors import ListedColormap X_set, y_set = X_train, y_train X1, X2 = np.meshgrid(np.arange(start = X_set[:, 0].min() - 1, stop = X_set[:, 0].max() + 1, step = 0.01), &nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp; &nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;np.arange(start = X_set[:, 1].min() - 1, stop = X_set[:, 1].max() + 1, step = 0.01)) plt.contourf(X1, X2, classifier.predict(np.array([X1.ravel(), X2.ravel()]).T).reshape(X1.shape), &nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp; alpha = 0.75, cmap = ListedColormap(('red', 'green', 'blue'))) plt.xlim(X1.min(), X1.max()) plt.ylim(X2.min(), X2.max()) for i, j in enumerate(np.unique(y_set)): &nbsp;&nbsp;&nbsp; plt.scatter(X_set[y_set == j, 0], X_set[y_set == j, 1], &nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp; c = ListedColormap(('red', 'green', 'blue'))(i), label = j) plt.title('Logistic Regression (Training set)') plt.xlabel('PC1') plt.ylabel('PC2') plt.legend() plt.show()</pre>
















&nbsp;
&nbsp;The graph will look like the following illustration:
&nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp;&nbsp;<img data-filename="2_PCA.png" style="width: 438px;" src="/uploads/tutorials/2019/08/05_2_PCA.png"> 
<pre># Visualising the Test set results from matplotlib.colors import ListedColormap X_set, y_set = X_test, y_test X1, X2 = np.meshgrid(np.arange(start = X_set[:, 0].min() - 1, stop = X_set[:, 0].max() + 1, step = 0.01), &nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp; np.arange(start = X_set[:, 1].min() - 1, stop = X_set[:, 1].max() + 1, step = 0.01)) plt.contourf(X1, X2, classifier.predict(np.array([X1.ravel(), X2.ravel()]).T).reshape(X1.shape), &nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp; alpha = 0.75, cmap = ListedColormap(('red', 'green', 'blue'))) plt.xlim(X1.min(), X1.max()) plt.ylim(X2.min(), X2.max()) for i, j in enumerate(np.unique(y_set)): &nbsp;&nbsp;&nbsp; plt.scatter(X_set[y_set == j, 0], X_set[y_set == j, 1], &nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp; c = ListedColormap(('red', 'green', 'blue'))(i), label = j) plt.title('Logistic Regression (Test set)') plt.xlabel('PC1') plt.ylabel('PC2') plt.legend() plt.show()</pre>
















The graph will look like the following: &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp;<img data-filename="3_PCA.png" style="width: 442px;" src="/uploads/tutorials/2019/08/05_3_PCA.png"> 
&nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp;&nbsp;

Principal Component Analysis

Linear Discriminant Analysis (LDA): Linear Discriminant Analysis(LDA) is a dimensionality reduction technique, that separates the best classes that are related to the dependent variable. Which makes it a supervised algorithm. In PCA, we do not consider the dependent variable. So this is the basic difference between the PCA and LDA algorithms.If there are n number of independent variables, the LDA algorithm will extract p&lt;=n new independent variables that separate most of the classes of the dependent variable.
LDA in Python: LDA is a very simple and popular algorithm in practice. In this tutorial, we will implement this algorithm alongside with <a href="http://www.aionlinecourse.com/tutorial/machine-learning/logistic-regression" target="_blank">Logistic Regression </a>algorithm. For this task, we will use the famous "Wine.csv" dataset from the UCI machine learning repository. Our version of dataset contains thirteen independent variables that represent various aspects of wines and one dependent variable that represent the three types of buyers of the wine based on specific features. Now, we will implement LDA to reduce the number of independent variables to a predefined value (i.e. two).You can download the whole dataset from <a href="https://www.dropbox.com/s/8139t6qk69wt10d/Wine.csv?dl=0" target="_blank">here.</a>&nbsp;You will get the full code in <a href="https://colab.research.google.com/drive/1Mnf3kL9JRF_C3PFPv522gt2jXpBXEM5H?usp=sharing" target="_blank">Google Colab</a> also.First of all, we will import some essential libraries.
<pre># Importing the libraries
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd</pre>


Then we will import our dataset and make the feature matrix and dependent variable vector.
<pre># Importing the dataset
dataset = pd.read_csv('Wine.csv')
X = dataset.iloc[:, 0:13].values
y = dataset.iloc[:, 13].values</pre>


Now, we will split the dataset into training and test sets.
<pre># Splitting the dataset into the Training set and Test set
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.2, random_state = 0)</pre>

Let's apply feature scaling onto the dataset.<pre># Feature Scaling
from sklearn.preprocessing import StandardScaler
sc = StandardScaler()
X_train = sc.fit_transform(X_train)
X_test = sc.transform(X_test)
</pre><div> </div>



We have come to the main part of our program. Now, we will implement the LDA algorithm to the dataset.
<pre># Applying LDA
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis as LDA
lda = LDA(n_components = 2)
X_train = lda.fit_transform(X_train, y_train)
X_test = lda.transform(X_test)</pre>
Note:&nbsp;n_component is the parameter that represents the number of independent variables we want in our model. Here we take it to 2, so our model will contain two independent variables.Let's fit a linear regression algorithm to our model.
<pre># Fitting Logistic Regression to the Training set
from sklearn.linear_model import LogisticRegression
classifier = LogisticRegression(random_state = 0)
classifier.fit(X_train, y_train)

# Predicting the Test set results
y_pred = classifier.predict(X_test)</pre> Now, let's see how well our model is to make predictions using the confusion matrix.
<pre># Making the Confusion Matrix
from sklearn.metrics import confusion_matrix
cm = confusion_matrix(y_test, y_pred)</pre><div>The confusion matrix will look like the following</div><div> </div><div>&nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp;<img data-filename="1_LDA.png" style="width: 321px;" src="/uploads/tutorials/2019/08/06_1_LDA.png"></div><div> </div><div>From the above confusion matrix, we can calculate the accuracy of our model and that comes out to be 100%!</div><div> </div>
Let's visualize the prediction of our model for both training and test sets.
<pre># Visualising the Training set results
from matplotlib.colors import ListedColormap
X_set, y_set = X_train, y_train
X1, X2 = np.meshgrid(np.arange(start = X_set[:, 0].min() - 1, stop = X_set[:, 0].max() + 1, step = 0.01),
 np.arange(start = X_set[:, 1].min() - 1, stop = X_set[:, 1].max() + 1, step = 0.01))
plt.contourf(X1, X2, classifier.predict(np.array([X1.ravel(), X2.ravel()]).T).reshape(X1.shape),
 alpha = 0.75, cmap = ListedColormap(('red', 'green', 'blue')))
plt.xlim(X1.min(), X1.max())
plt.ylim(X2.min(), X2.max())
for i, j in enumerate(np.unique(y_set)):
 plt.scatter(X_set[y_set == j, 0], X_set[y_set == j, 1],
 c = ListedColormap(('red', 'green', 'blue'))(i), label = j)
plt.title('Logistic Regression (Training set)')
plt.xlabel('LD1')
plt.ylabel('LD2')
plt.legend()
plt.show()</pre>















 The graph will look like the following illustration &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp;<img data-filename="2_LDA.png" style="width: 439px;" src="/uploads/tutorials/2019/08/06_2_LDA.png"> 
<pre># Visualising the Test set results
from matplotlib.colors import ListedColormap
X_set, y_set = X_test, y_test
X1, X2 = np.meshgrid(np.arange(start = X_set[:, 0].min() - 1, stop = X_set[:, 0].max() + 1, step = 0.01),
 np.arange(start = X_set[:, 1].min() - 1, stop = X_set[:, 1].max() + 1, step = 0.01))
plt.contourf(X1, X2, classifier.predict(np.array([X1.ravel(), X2.ravel()]).T).reshape(X1.shape),
 alpha = 0.75, cmap = ListedColormap(('red', 'green', 'blue')))
plt.xlim(X1.min(), X1.max())
plt.ylim(X2.min(), X2.max())
for i, j in enumerate(np.unique(y_set)):
 plt.scatter(X_set[y_set == j, 0], X_set[y_set == j, 1],
 c = ListedColormap(('red', 'green', 'blue'))(i), label = j)
plt.title('Logistic Regression (Test set)')
plt.xlabel('LD1')
plt.ylabel('LD2')
plt.legend()
plt.show()&nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp;&nbsp;</pre>&nbsp; &nbsp;&nbsp;The output graph will be- &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp;&nbsp;<img data-filename="3_LDA.png" style="width: 438px;" src="/uploads/tutorials/2019/08/06_3_LDA.png">

Linear Discriminant Analysis (LDA)

Kernel Principal Component Analysis(Kernel PCA): Principal component analysis (PCA) is a popular tool for dimensionality reduction and feature extraction for a linearly separable dataset. But if the dataset is not linearly separable, we need to apply the Kernel PCA algorithm. It is similar to PCA except that it uses one of the kernel tricks to first map the non-linear features to a higher dimension, then it extracts the principal components as same as PCA.Kernel PCA in Python: In this tutorial, we are going to implement the Kernel PCA alongside with a Logistic Regression algorithm on a nonlinear dataset. For this task, we will use the "Social_Network_Ads.csv" dataset. In the dataset, the features have a non-linear correlation with the dependent variable. So, we have to apply Kernel PCA to extract the independent variables. Let's have a glimpse of that dataset.

&nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp;&nbsp;<img data-filename="4_Kernel_PCA.png" style="width: 476px;" src="/uploads/tutorials/2019/08/07_4_Kernel_PCA.png"> You can download the whole dataset from<a href="https://www.dropbox.com/s/sj2r3og9br7z08j/Social_Network_Ads.csv?dl=0" target="_blank"> here.</a>First of all, Let's import the essential libraries. You will get the code in <a href="https://colab.research.google.com/drive/1BRbzPRc3SKhGD7q7FVDdVuhi97eLdvjl?usp=sharing" target="_blank">Google Colab</a> also.<pre style="font-size: 14px;">import numpy as np
import matplotlib.pyplot as plt
import pandas as pd</pre>Importing the dataset<pre style="font-size: 14px;">dataset = pd.read_csv('Social_Network_Ads.csv') X = dataset.iloc[:, [2, 3]].values y = dataset.iloc[:, 4].values</pre> Splitting the dataset into the Training set and Test set <pre style="font-size: 14px;">from sklearn.model_selection import train_test_split X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.25, random_state = 0)</pre> &nbsp;Feature Scaling<pre style="font-size: 14px;">from sklearn.preprocessing import StandardScaler sc = StandardScaler() X_train = sc.fit_transform(X_train) X_test = sc.transform(X_test)</pre> Applying Kernel PCA<pre style="font-size: 14px;">from sklearn.decomposition import KernelPCA kpca = KernelPCA(n_components = 2, kernel = 'rbf') X_train = kpca.fit_transform(X_train) X_test = kpca.transform(X_test)</pre>Note:&nbsp;Here,&nbsp;n_components&nbsp;parameter defines the number of independent variables we want in our model (here, it is two) and we choose RBF(Radial Basis Function) kernel as our kernel function.&nbsp;Fitting Logistic Regression to the Training set<pre style="font-size: 14px;">from sklearn.linear_model import LogisticRegression classifier = LogisticRegression(random_state = 0) classifier.fit(X_train, y_train)</pre> Predicting the Test set results<pre style="font-size: 14px;">y_pred = classifier.predict(X_test)</pre> Making the Confusion Matrix<pre style="font-size: 14px;">from sklearn.metrics import confusion_matrix cm = confusion_matrix(y_test, y_pred)</pre> &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp;<img data-filename="1_Kernel_PCA.png" style="width: 555px;" src="/uploads/tutorials/2019/08/07_1_Kernel_PCA.png"> From the above confusion matrix, we can see that the model has an accuracy of 80%Now, let's visualize both the training and test set results.Visualising the Training set results<pre style="font-size: 14px;">from matplotlib.colors import ListedColormap X_set, y_set = X_train, y_train X1, X2 = np.meshgrid(np.arange(start = X_set[:, 0].min() - 1, stop = X_set[:, 0].max() + 1, step = 0.01), &nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;np.arange(start = X_set[:, 1].min() - 1, stop = X_set[:, 1].max() + 1, step = 0.01)) plt.contourf(X1, X2, classifier.predict(np.array([X1.ravel(), X2.ravel()]).T).reshape(X1.shape), &nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;alpha = 0.75, cmap = ListedColormap(('red', 'green'))) plt.xlim(X1.min(), X1.max()) plt.ylim(X2.min(), X2.max()) for i, j in enumerate(np.unique(y_set)): &nbsp;&nbsp;&nbsp;plt.scatter(X_set[y_set == j, 0], X_set[y_set == j, 1], &nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;c = ListedColormap(('red', 'green'))(i), label = j) plt.title('Logistic Regression (Training set)') plt.xlabel('Age') plt.ylabel('Estimated Salary') plt.legend() plt.show()</pre>The graph will look like the following:&nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp;&nbsp;<img data-filename="2_Kernel_PCA.png" style="width: 452px;" src="/uploads/tutorials/2019/08/07_2_Kernel_PCA.png">&nbsp; &nbsp;Visualising the Test set results<pre style="font-size: 14px;">from matplotlib.colors import ListedColormap X_set, y_set = X_test, y_test X1, X2 = np.meshgrid(np.arange(start = X_set[:, 0].min() - 1, stop = X_set[:, 0].max() + 1, step = 0.01), &nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;np.arange(start = X_set[:, 1].min() - 1, stop = X_set[:, 1].max() + 1, step = 0.01)) plt.contourf(X1, X2, classifier.predict(np.array([X1.ravel(), X2.ravel()]).T).reshape(X1.shape), &nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;alpha = 0.75, cmap = ListedColormap(('red', 'green'))) plt.xlim(X1.min(), X1.max()) plt.ylim(X2.min(), X2.max()) for i, j in enumerate(np.unique(y_set)): &nbsp;&nbsp;&nbsp;plt.scatter(X_set[y_set == j, 0], X_set[y_set == j, 1], &nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;c = ListedColormap(('red', 'green'))(i), label = j) plt.title('Logistic Regression (Test set)') plt.xlabel('Age') plt.ylabel('Estimated Salary') plt.legend() plt.show()</pre>The graph will look like the following:&nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp;<img data-filename="3_Kernel_PCA.png" style="width: 447px;" src="/uploads/tutorials/2019/08/07_3_Kernel_PCA.png">

Kernel PCA

Model Selection &amp; Boosting: Model Selection is the undertaking of choosing a statistical model from an arrangement of candidate models, given information. In the least difficult cases, a prior arrangement of information is considered. Boosting is a machine learning ensemble meta-algorithm for essentially lessening inclination, and furthermore changes in supervised learning, and a group of machine learning algorithms which change over weak learners to strong ones. Types of Boosting Algorithms are:
1. &nbsp;&nbsp; AdaBoost (Adaptive Boosting)
2. &nbsp;&nbsp; Gradient Tree Boosting
3. &nbsp;&nbsp; XGBoost

Model Selection & Boosting

Evaluation of machine learning models is important. To build a state of the art machine learning model, you need to make sure the accuracy of your model on every test set is as good as the accuracy it has obtained from the training set.
Usually, we take a data set, split it into train and test sets. We use the training set to train the model and the test set to evaluate the performance of the model. But it is not a good approach as in production, the model would come across data quite different from the test set. Which eventually lead to degrading the performance of the model, making our evaluation faulty.
To solve this problem, we can use cross-validation techniques such as k-fold cross-validation.&nbsp;Cross-validation is a statistical method used to compare and evaluate the performance of Machine Learning models.
In this tutorial, we are going to learn the K-fold cross-validation technique and implement it in Python. Let's dive into the tutorial!
<h4>What is K-fold Cross Validation?</h4>
While building machine learning models, we randomly split the dataset into training and test sets where a maximum percentage of the data is taken into the training set. Though the test dataset is small, there is still some chance that we left some important data in there that might have improved the model. And there is a problem of high variance in the training set. Here where the idea of K-fold cross-validation comes in handy. In K-fold Cross-Validation, the training set is randomly split into K(usually between 5 to 10) subsets known as folds. Where K-1 folds are used to train the model and the other fold is used to test the model. This technique improves the high variance problem in a dataset as we are randomly selecting the training and test folds.
<img src="/uploads/tutorials/2019/08/24_1_k-fold_cross_validation.png" alt="24_1_k-fold_cross_validation"> The steps required to perform K-fold cross-validation are given below-
Step 1: Split the entire data randomly in k folds(usually between 5 to 10). The higher number of splits leads to a less biased model. Step 2: Then fit the model with k-1 folds and test it with the remaining Kth fold. Record the performance metric. Step 3: Repeat step 2 until every k-fold serves as the test set. Step 4: Take the average of all the recorded scores. This will serve as the final performance metric of your model.
<h4>Implementing K-fold Cross Validation in Python</h4>Now, we will implement this technique to validate our machine-learning model. For this task, we are using "Social_Network_Ads.csv" dataset.
You can download the dataset from&nbsp;<a href="https://www.dropbox.com/s/sj2r3og9br7z08j/Social_Network_Ads.csv?dl=0">here.</a>
This is a classification task. And for this, we will build a Kernel SVM classification model. You will get the code in <a href="https://colab.research.google.com/drive/1fu_Yq3y5j_qU59_gd4siq0VrxJgmV950?usp=sharing" target="_blank">Google Colab</a> also.
First, we will use the conventional method, randomly split the dataset into training and test set, train the model, and evaluate it on the test set.
Then We will implement the K-fold cross-validation technique to improve our model.
First of all, we need to import some essential libraries.<pre># Importing the libraries 
import numpy as np 
import matplotlib.pyplot as plt 
import pandas as pd
</pre>Now, we will import the dataset and make the feature matrix X and the dependent variable vector y.<pre># Importing the dataset 
dataset = pd.read_csv('Social_Network_Ads.csv') 
X = dataset.iloc[:, [2, 3]].values 
y = dataset.iloc[:, 4].values
</pre>Now, we will split the dataset into training and test sets.<pre># Splitting the dataset into Training set and Test set 
from sklearn.model_selection import train_test_split 
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.25, random_state = 0)
</pre>We, need to feature scale our training and test sets for an improved result.<pre># Feature Scaling 
from sklearn.preprocessing import StandardScaler 
sc = StandardScaler() 
X_train = sc.fit_transform(X_train) 
X_test = sc.transform(X_test)
</pre>Now, we will fit Kernel SVM into our training set and predict how it performs on the test set.&nbsp;<pre># Fitting Kernel SVM to the Training set 
from sklearn.svm import SVC 
classifier = SVC(kernel = 'rbf', random_state = 0) 
classifier.fit(X_train, y_train) 

# Predicting the Test set results y_pred = classifier.predict(X_test)
</pre>To calculate the accuracy of our Kernel SVM model we will build the confusion matrix.<pre># Making the Confusion Matrix 
from sklearn.metrics import confusion_matrix 
cm = confusion_matrix(y_test, y_pred)
</pre>&nbsp;Let's see how accurate our model is &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp;&nbsp;<img src="/uploads/tutorials/2019/08/24_2_K_fold_Cross_Validation_(2).png" alt="24_2_K_fold_Cross_Validation_(2)">
From the above matrix, we can see that the accuracy of our Kernel SVM model is 93% Now, let's see how we can improve the performance metric of our model using K-fold cross-validation with k = 10 folds.&nbsp;<pre># Applying k-Fold Cross Validation 
from sklearn.model_selection import cross_val_score 
accuracies = cross_val_score(estimator = classifier, X = X_train, y = y_train, cv = 10) 
accuracies.mean() 
accuracies.std()
</pre>Let's see the accuracies for all the folds. &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp;<img src="/uploads/tutorials/2019/08/24_5_K_fold_Cross_Validation.png" alt="24_5_K_fold_Cross_Validation">The mean value for the accuracies is 90% with a mean deviation of 6%. That means our model is accurate for 96% or 84% time.
<h4>Choosing the Number of Folds&nbsp;</h4>
It depends on how much CPU power you have or willing to spend. A lower value of K means less variance which leads to more bias. And having a higher value means more variance and lower bias.&nbsp;
The computational cost for different values is the primary concern while choosing the value. A higher K value requires more computational time and power and vice versa. Lowering down folds value will not be helpful to find the most performing model and taking a higher value will take a longer time to completely train the model.
So, you need to find a spot where the cost and performance tradeoff gets to an equilibrium state. This can be done during hyper tuning analysis.&nbsp;
Finally, the most important thing is the size of your data. If the amount of data is small, using a k-fold cross-validation scheme would not make any sense. And if the amount of data is large, you must give efforts to choose the perfect value of K.
<h4>Types of Cross Validation&nbsp;</h4>
There are several variants of k fold cross-validation, used for different purposes. Many variants are implemented in the Scikit-Learn library. Some of the most widely used cross-validation techniques are-
<ul><li>Repeated K fold Here the k-folds repeats itself n times. If you need to run KFold n times, you can implement this class from sklearn library. It will produce different splits in each repetition.</li>
 <li>Leave One Out Cross Validation(LOOCV) It is a simple cross-validation technique. Each training set contains all the samples except one. This one sample is used taken to the test set. Thus, we have different training sets and test sets for samples. It is a good choice for small data sets. This technique ensures more variance in the test set and lowers bias in the model.</li>
 <li>Shuffle and Split Like the k fold cross-validation, where a user defines a value of k for the number of folds. The process first shuffles the samples and then splits them into a pair of training and test set for each fold. The user can control the randomness for reproducibility.</li>
 <li>Stratified K Fold It is a variation of k fold that returns stratified folds. Here the 'stratified' represents the preservation of the&nbsp;percentage of samples for each class. Each fold contains approximately the same percentage of samples of each target class as the complete set. This method ensures the exact or as close as possible distribution of classes across all the folds.</li>
 <li>Time Series Split It is a special variation of k fold cross-validation to validate time series data samples, observed at fixed time intervals. It returns first k folds as train set and the (k+1) th set as test set. Unlike conventional k fold cross-validation methods,&nbsp;successive training sets are supersets of those that come before them. It also adds all surplus data to the first training set that is always used to train the model.</li>
</ul><h4>Advantages and Disadvantages of K fold Cross</h4>
There are some advantages of k fold cross-validation with over validation techniques. There are some disadvantages as well. Let's have a look at them.
<h5>Advantages</h5>
<ul><li>Better Model Accuracy Using k-fold cross validation you will get a more accurate model than using just a random split of data set into train and test sets.</li>
 <li>Reduce Overfitting When you are using cross-validation, the model is rigorously trained and tested along the way. So, the data you give to the model will be distributed in a more proper way than just a train and test method. This will make the model less overfitted to the train set, eventually giving an improved performance on unseen data.&nbsp;&nbsp;</li>
 <li>Better Hyperparameter Tuning Hyperparameter tuning methods such as grid search and random search with k fold cross-validation are more powerful than without cross-validation. You should use hyperparameter tuning methods with cross-validation for better performance.</li>
 <li>
 Better Feature Extraction Cross-validation can be used to extract the most important features of a data set. Reverse Feature Extraction with Cross-Validation(<a href="https://scikit-learn.org/stable/modules/generated/sklearn.feature_selection.RFECV.html">RFECV</a>) is a method that uses cross-validation while extracting the best features for a machine learning model.
 </li>
 <li>Improved Models for Imbalanced Data K fold cross-validation methods are very handy for imbalanced data. As the data is equally split among the train and test sets, the distribution of the data will be balanced, eventually leading to a better performing model.</li>
</ul><h5>Disadvantages&nbsp;</h5>
<ul><li>Computational Cost Doing cross-validation will require extra time. If you choose cross-validation methods like LOOCV for large data samples, the computational overhead will be high. But using like 5 fold or 10 fold cross-validation would not take much time. And the performance will be quite satisfactory.</li>
 <li>Bad with Sequential Data If you are working with sequential data such as time-series data, k fold cross-validation is a bad choice. Because it does not work well with sequential data due to its nature. In time series, you need to predict the future value based on a series of past values of your data. Under this constraint, k fold will be failed to perform well. But you can use the time-series split, a variation of k fold, to cross-validate the time series model.</li>
</ul><h4>Comparison with Other Validation Method</h4>
There is a continuous debate on which method of validation is best for a model. Most of the time it is k fold. Let's compare k fold with other validation methods.
<h5>Holdout Vs. K fold Cross-Validation</h5>
In the holdout method, we split the data set into train and test sets. The model is trained on the train set and then evaluated by the test set. The method is simple and easy to implement. But not a better indicator of the performance of your model. As cross-validation uses multiple splits for train and test sets, it gives you a better indication of the performance of your model on unseen data.
The holdout method comes in handy when you are using a large data set or you are in short of time as cross-validation incurs more computational cost. But yet you should apply cross-validation whenever possible instead of the holdout method.&nbsp;
<h5>K fold Cross Validation Vs. Bootstrap</h5>
In the bootstrapping method, the data set is resampled at random to make several data sets so that the model can be evaluated with a wide number of data samples. The method samples the original data and takes the 'not chosen' samples as test cases. Then the average accuracy score is taken as the estimation of the model performance.
In essence, the bootstrap method can be seen more as a variance/bias estimation rather than a validation technique. It is useful in ensemble methods such as a random forest as it can create multiple data sets from the original data. We can use each bootstrap data set for building a number of single models (e.g. a decision tree) and combine all models with an ensemble model. Then we will take the majority voting of all these single models to get our final model performance.&nbsp;
On the other hand, k fold cross-validation splits the original data set to rigorously train and test the model.&nbsp;
In this sense, we can see that bootstrapping is not the right kind of evaluation model like k fold cross-validation. We still need k fold to evaluate the model's performance. The bootstrap method will be a weaker evaluation technique if used alone.
<h4>Final Words</h4>
In this tutorial, I tried to explain all the important aspects of k fold cross-validation. In summary, the key take ways of the tutorial are-
<ul><li>What is k fold cross-validation and why it is necessary for model evaluation</li>
 <li>Implementation in Python</li>
 <li>Advantages and disadvantages of cross-validation</li>
 <li>Comparison of k fold cross-validation with other validation methods</li>
</ul>Hope the tutorial has served you the concepts well. Do you have any questions about the concepts of the tutorial? Please let me know in the comments. You can also give feedback to improve the tutorial. I will gladly accept any new idea to make things better.
Happy Machine Learning!

K-fold Cross Validation in Python | Master this State of the Art Model Evaluation Technique

XGBoost in Python Step 1: First of all, we have to install the XGBoost. Now, we need to implement the classification problem. In this problem, we classify the customer into two classes and who will leave the bank and who will not leave the bank. Now, we import the library and we import the dataset churn Modeling csv file. So, we just want to preprocess the data for this churn modeling problem associated with this churn modeling CSV file. Here, XGboost is a great and boosting model with decision trees according to the feature skilling. After building the model, we can understand, XGBoost is so popular because of three qualities, the first quality is high performance and the second quality is fast execution speed. Now, we split the dataset into the training set and testing set. You will get the python code in <a href="https://colab.research.google.com/drive/1Tk3Ny70JF6SEs9fwm6kPG1GG55paN23k?usp=sharing" target="_blank">Google Colab</a> also.
<pre>import numpy as np import matplotlib.pyplot as plt import pandas as pd</pre>
# Importing the dataset
<pre>dataset = pd.read_csv('Churn_Modelling.csv') X = dataset.iloc[:, 3:13].values y = dataset.iloc[:, 13].values</pre>
# Encoding categorical data
<pre># Encoding categorical data
from sklearn.preprocessing import LabelEncoder, OneHotEncoder, OrdinalEncoder
from sklearn.compose import ColumnTransformer
# Country column
ct = ColumnTransformer([("Country", OneHotEncoder(), [1]), ("Gender", OrdinalEncoder(), [2])], remainder = 'passthrough')
X = ct.fit_transform(X)</pre>
# Splitting the dataset into the Training set and Test set
<pre>from sklearn.model_selection import train_test_split X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.2, random_state = 0)</pre>

 
XGBoost in Python Step 2: In this tutorial, we gonna fit the XSBoost into the training set. Now, we apply the xgboost library and import the XGBClassifier.Now, we apply the classifier object. And we call the XGBClassifier class. Now, we apply the fit method. Now, we execute this code. Now, we apply the confusion matrix. And we also predict the test set result. And we applying the k fold cross validation code. Now, we execute this code. After executing this code, we get the dataset. Then we get the confusion matrix, where we get the 1521+208 correct prediction and 197+74 incorrect prediction. And we get this accuracy of 86%. After executing the mean&nbsp;function, we get 86%.
<pre>from xgboost import XGBClassifier classifier = XGBClassifier() classifier.fit(X_train, y_train)</pre>


 
# Predicting the Test set results
<pre>y_pred = classifier.predict(X_test)</pre>
 
# Making the Confusion Matrix
<pre>from sklearn.metrics import confusion_matrix cm = confusion_matrix(y_test, y_pred)</pre>

 
# Applying k-Fold Cross Validation
<pre>from sklearn.model_selection import cross_val_score accuracies = cross_val_score(estimator = classifier, X = X_train, y = y_train, cv = 10) accuracies.mean() accuracies.std()</pre>

XGBoost

Convolution Neural Network: A Convolutional neural network (CNN, or ConvNet) is a class of deep, feed-forward artificial neural networks, most commonly applied to analyzing visual imagery.
CNN's use a variation of multilayer perceptrons designed to require minimal preprocessing. They are also known as shift invariant or space invariant artificial neural networks (SIANN), based on their shared-weights architecture and translation invariance characteristics.
Convolutional networks were inspired by biological processes in that the connectivity pattern between neurons resembles the organization of the animal visual cortex. Individual cortical neurons respond to stimuli only in a restricted region of the visual field known as the receptive field. The receptive fields of different neurons partially overlap such that they cover the entire visual field.
CNN uses relatively little pre-processing compared to other image classification algorithms. This means that the network learns the filters that in traditional algorithms were hand-engineered. This independence from prior knowledge and human effort in feature design is a major advantage.
Here, we have an image, convolution neural network and having output label image.<img data-filename="cnn_1.png" style="width: 674px;" src="/uploads/tutorials/2018/09/21_cnn_1.png"><img data-filename="cnn_2.png" style="width: 273px;" src="/uploads/tutorials/2018/09/21_cnn_2.png"> 

 

Convolution Operation: In this tutorial, we are going to talk about convolution. Here, we describe the convolution function:
<img data-filename="cnn_3.png" style="width: 500px;" src="/uploads/tutorials/2018/09/21_cnn_3.png"> 

Convolution is a combined integration of the two functions and it shows you how one function modifies the other or modifies the shape of the other.
Convolution is a mathematical operation to merge two sets of information. In our case, the convolution is applied to the input data using a convolution filter to produce a feature map. There are a lot of terms being used so let's visualize them one by one.
On the left side is the input to the convolution layer, for example, the input image. On the right is the convolution filter, also called the kernel, we will use these terms interchangeably. This is called a 3x3 convolution due to the shape of the filter.
We perform the convolution operation by sliding this filter over the input. At every location, we do element-wise matrix multiplication and sum the result. This sum goes into the feature map. Now, we have some input messages and we create a feature map. We create multiple feature maps because we use different filters.
 

<img data-filename="cnn_4.png" style="width: 644px;" src="/uploads/tutorials/2018/09/21_cnn_4.png"> 
ReLU &nbsp;Layer: In this tutorial, we are going to talk about the ReLU layer. Here, we are applying the rectifier because we want to increase non-linearity in our image. They propose different types of rectified functions.
 
Pooling: In this tutorial, we are going to talk about the max pooling.
 
Max pooling is a sample-based discretization process. The objective is to down-sample an input representation (image, hidden-layer output matrix, etc.), reducing its dimensionality and allowing for assumptions to be made about features contained in the sub-regions binned.
This is done so in part to help over-fitting by providing an abstracted form of the representation. As well, it reduces the computational cost by reducing the number of parameters to learn and provides basic translation invariance to the internal representation.
Max pooling is done by applying a max filter to (usually) non-overlapping subregions of the initial representation.
We are taking the maximum of the pixel that we or the values that we have. This helping with preventing&nbsp;overfitting. We applied the convolution operation and now we apply the pooling.<img data-filename="cnn_5.png" style="width: 688px;" src="/uploads/tutorials/2018/09/21_cnn_5.png"> 

Flattening: Here, we have the pooled featured map. After that, we apply the convolution operation to our image and then we apply the pooling to the result of the collision. So, we are going to flatten it into the column. Here, we see many pooling layers. We put them into one log column sequentially. In the input image, we apply the convolution. And also apply the rectifier function.

<img data-filename="cnn_6.png" style="width: 691px;" src="/uploads/tutorials/2018/09/21_cnn_6.png"> 
Full Connection: Today, we are talking about the full connection. In this step, we are adding a whole artificial neural network to our convolutional neural network. Here, we are calling them fully connected which are the hidden layer. The main purpose of the artificial neural network to combine our features into more attributes. Here, we used to call a cost function in an artificial neural network and we used mean square error there is a common illusional neural network. It is called a loss function and we use the across entropy function for that. We are trying to optimize it to minimize that function to optimize our network. We had an artificial neural network that is backpropagated and some things are adjusted t help optimize. It all done through gradient descent of backpropagation. The dog neuron knows that the answer is actually a dog because at the end we are comparing to the picture or to the label on the picture.
 
CNN in Python 1: In this tutorial, we are going to implement CNN in python. Here, we build our convolutional neural network model, we will simply need to change the image of
Then, we will be able to train a convolutional neural network to predict if some new brain image contains the tumor is yes or no. Now, we have to input these images in our convolution neural that work.
Here, in the working directory, we have a dataset that is all our images of cats and dogs. In each folder the training set and the test set we would get for example 5000 images.
The first pillar of the structure is to separate our images into two separate folders. A training set folder and testing set folder. Here, we see different dog pictures. Now, we can take some pictures of our friends and replace these dogs' pictures with that picture. Then, we will able to train an algorithm that will predict. And, there are images of a cat. Here, the training set contained 8000 customers and the test set contained 2000 customers. Here, also,4000 images for dogs and 4000 images for cats. So, there are an 80 percent and 20 percent split. We already import this dataset. we do not need to encode the dataset because the independent variable is some way of a pixel and the three-channel. We need to split the dataset into the training set and test set. Now, we need to apply the feature scaling. You will get the code in <a href="https://colab.research.google.com/drive/1vgPe4DUxK8UpdfL1vYk_aA7bziFt19cP?usp=sharing" target="_blank">Google Colab</a> also.
 
<pre># Importing the libraries
import tensorflow as tf
from keras.preprocessing.image import ImageDataGenerator</pre>


 
# Downloading the datasetYou can download the dataset zip from <a href="https://drive.google.com/file/d/1JbnFhkLNWupjWHCGt56ASU27ixoNUuzI/view?usp=sharing" target="_blank">here</a> with 5000 pictures and train and test datasets. Download the zip file and extract it in your project directory.&nbsp; 
CNN in Python 2: In this tutorial, we are going to talk about the convolution neural network. The first step is to import all the Keras packages that we will need to make our CNN model. Here, the first package is sequential. We use sequential packages to initialize our neural network. Now, we import convolution layers and we are working on images and since images are in two dimensions. We use the 2D packages to deal with images. And we also add our pooling layers. And next is flatten. Here, we also use the last dense packages. We use to add fully connected layers and a classic artificial neural network. Now, I execute the code.
Now, we are going to create an object of this sequential class. We are going to call this object classifier and we call the sequential method.
 
<pre>from keras.models import Sequential from keras.layers import Convolution2D from keras.layers import MaxPooling2D from keras.layers import Flatten from keras.layers import Dense</pre>




CNN in Python 3:&nbsp;Now, we are going to preprocess our data. Here we will preprocess our train set and test set.
<pre># Preprocessing the Training set
train_datagen = ImageDataGenerator(rescale = 1./255,
 shear_range = 0.2,
 zoom_range = 0.2,
 horizontal_flip = True)
training_set = train_datagen.flow_from_directory('dataset/training_set',
 target_size = (64, 64),
 batch_size = 32,
 class_mode = 'binary')
</pre>
<pre># Preprocessing the Test set
test_datagen = ImageDataGenerator(rescale = 1./255)
test_set = test_datagen.flow_from_directory('dataset/test_set',
 target_size = (64, 64),
 batch_size = 32,
 class_mode = 'binary')
</pre>
&nbsp; CNN in Python 4: In this tutorial, we are going to take care of the first state of convolutions. Here, we take the classifier object and also include the method add. Here, we include convolution2D. Here, we use the 32 feature detectors three by three-dimension for feature detectors. We need to specify what are the expected format of our input images. The input image converted into a 3D array if the image is a color image and into a 2D array if it is a black and white image. The 3D means three-channel. We need to start with the 2D array dimension. We need to import here for our input shape argument. Therefore, 64 to 64 and then the number of channel 3 that is we are using tensor flow. We have one last argument to input which is the activation function exactly as we did for our fully connected layers. We used this activation function to activate the neurons in the neural network. Here, we are using the rectifier function.
 
# Initialising the CNN
<pre>cnn = tf.keras.models.Sequential()</pre>
 
# Step 1 - Convolution
<pre>cnn.add(tf.keras.layers.Conv2D(filters=32, kernel_size=3, activation='relu', input_shape=[64, 64, 3]))</pre>
 
CNN in Python 5: Today, we will take care of the second step pulling. We call the classifier. For the classifier object, we use the add method. And we add the new parenthesis max pooling. We use the max pool size 2 and 2.This line will reduce the size of our maps and it's well divided by two. The size of the feature map is divided by two. For flattening, we use the classifier object and use the add method. We use the parenthesis Flatten().
In the same way, For Full connection, we use the classifier object and use the add method. We use the parenthesis Dense (). Also has a parenthesis output_dim is equal to 128. We need to choose a number that is not too small to make the classifier a good model and also not too big. Here, we will go with these 128 hidden nodes in the hidden layer. And another activation function is a rectifier. Now, we copy-paste the code. And, add the sigmoid function. now, we add 128 to 1. Then, we get the final layer, which predicts the output.
 
# Step 2 - Pooling
<pre>cnn.add(tf.keras.layers.MaxPool2D(pool_size=2, strides=2))</pre>
# Adding a second convolutional layer
<pre>cnn.add(tf.keras.layers.Conv2D(filters=32, kernel_size=3, activation='relu'))
cnn.add(tf.keras.layers.MaxPool2D(pool_size=2, strides=2))</pre>

 
# Step 3 - Flattening
<pre>cnn.add(tf.keras.layers.Flatten())</pre>
 
# Step 4 - Full connection
<pre>cnn.add(tf.keras.layers.Dense(units=128, activation='relu')) </pre>
# Step 5 - Output Layer
<pre>cnn.add(tf.keras.layers.Dense(units=1, activation='sigmoid')) </pre>

 
CNN in Python 8: In this tutorial, we need to compile the whole thing by choosing to cast a grade. To compile this, we add the compile method and also add the parameter in the optimizer. The optimizer is equal to Adam. Ans we use loss is equal to bunary_cross entropy. And, the metrics are equal to the accuracy.
 
# Compiling the CNN
<pre>cnn.compile(optimizer = 'adam', loss = 'binary_crossentropy', metrics = ['accuracy'])</pre>
# Training the CNN on the Training set and evaluating it on the Test set
<pre>cnn.fit(x = training_set, validation_data = test_set, epochs = 25)</pre>
 
CNN in Python 9: In this tutorial, we are going to fit the CNN image. We actually need a lot of images to find and generalize some correlations. The amount of our training images is augmented because the transformation is a random transformation. Image augmentation is a technique that allows you to enrich our dataset our train set. Now, image augmentation is applied to the training set. Here, we create ImageDataGenerator class. We will rescale all our pixel values between 0 and 1. By rescaling them using this rescale equals one over 255 then all our pixels will be between 0 and 1. She arranged that to apply random transaction and we will keep this open to value zoom range. So these 0.2 values here are just some parameters of how much we want to apply these random transformations. We call it the test set because this code section will create the test set. We have 8000 images in our training set. we need to replace 2000 with 8000 right. Now, we generate a fit method for our classifier. Now, we execute it. And we create another object. Here, 8000 and 2000 images belonging to two classes.2000 image of our test set. After execution, we get 75% accuracy. We get three predictions out of four..there is a difference between the accuracy in the training set and accuracy in the test set.
 
<pre>import numpy as np
from keras.preprocessing import image
test_image = image.load_img('dataset/single_prediction/cat_or_dog_1.jpg', target_size = (64, 64))
test_image = image.img_to_array(test_image)
test_image = np.expand_dims(test_image, axis = 0)
result = cnn.predict(test_image)
training_set.class_indices
if result[0][0] == 1:
 prediction = 'dog'
else:
 prediction = 'cat'
print(prediction)</pre> 
CNN in Python 10: In this tutorial, we are going to talk about if we achieve our goal to get an accuracy of more than 80 percent on the test. Only adding a convolutional layer, we will see how it will definitely improve our performance results. Now, we add another convolution layer. Here, we going to keep the same parameter. Now, we execute the whole code. The accuracy of the training set is about 85. The accuracy of stains on the test began at 55 percent almost 56 percent. We got indeed 64 percent and 68 percent on the test set. We get an accuracy of 85 percent for the training set and 82 percent for the test. We get a difference of 3 percent as opposed to this 10 percent difference that we got in.
 
Softmax and Cross-Entropy: In softmax function in order to help us out of the situation.
<img data-filename="cnn_7.png" style="width: 429px;" src="/uploads/tutorials/2018/09/21_cnn_7.png"> 

The softmax function or the normalized exponential function is a generalization of the logistic function. It takes the exponent and puts the power of zed and adds it up so that one's two across all. Here we use a function called the mean squared which we used as the cost function for assessing our natural performance. Our goal is to minimize the MSE in order to optimize our network performance.

<img data-filename="cnn_8.png" style="width: 502px;" src="/uploads/tutorials/2018/09/21_cnn_8.png">

Convolution Neural Network

Think of working with a dataset with hundreds of features. Intuitively you can understand the hardship you must deal with while visualizing the dataset or training your model with it. This is because of the dimensions it would take as a higher number of features will lead to higher dimensions. And higher dimensions are not suitable for visualizing the dataset for a more intuitive understanding of the problem.
 
Overfitting will be another issue related to high dimensionality. This is because many of the features are somehow correlated to some fashion. Hence most of the features are redundant. For example, if you have to predict the weather where rainfall and humidity are two of the features, you can see two of them are somehow correlated. To avoid overfitting you need to reduce the features for the sake of getting better prediction accuracy.
 
This is where dimensionality reduction techniques come into play. This is simply reducing the dimension of your feature set. This technique allows you to find a small set of most impactful features among a large number of features. With this small set of principal features, you can run your prediction algorithms easily with better accuracy.
 
<h5>Why Do We Need Dimensionality Reduction Techniques?</h5><h5> </h5>
<ul><li>
 With less number of dimensions the space required to store the data is reduced
 </li>
 <li>
 Training time also accelerated due to lower dimensions
 </li>
 <li>
 Some algorithms such as Decision Tree and SVM do not perform well with higher dimensions. So, we need fewer dimensions for better accuracy with these models.
 </li>
 <li>
 It removes the multicollinearity problem that happens due to highly correlated features in the dataset.
 </li>
 <li>
 It reduces the complexity of visualizing the data. As you can understand that a plot is more intuitive in 2D than in a 3D form.
 </li>
</ul> 
There are two different dimensionality reduction techniques:
<ol><li>
 Feature Selection Methods
 </li>
 <li>
 Feature Extraction Methods
 </li>
</ol> 
<h5>Feature Selection Methods</h5>
Feature selection methods use the statistical relationship of input variables to the output variable. The methods mainly find the correlations among the features and try to select the most independent features that have no colinearity. It selects the features with the highest importance.&nbsp;
Some of the common feature selection techniques are-
<ul><li>
 Filter Methods
 </li>
 <li>
 Wrapper Methods
 </li>
 <li>
 Embedded Methods
 </li>
</ul>Filter Methods: In this method, each feature is ranked based on some univariate metrics. Then it selects the highest-ranking features.&nbsp;
Some of the common filtering methods are-
<ul><li>
 variance
 </li>
 <li>
 chi-square
 </li>
 <li>
 correlation coefficients
 </li>
 <li>
 information gain or mutual information</li></ul>Wrapper Methods: Wrapper methods selects the features based on specific classifier performance. With a greedy approach, it evaluates all the possible combinations of features against the evaluation criterion.
Some of the popular wrapper methods are-
<ul><li>
 recursive feature elimination
 </li>
 <li>
 sequential feature selection algorithms
 </li>
 <li>
 genetic algorithms
 </li>
</ul>Embedded Methods: These methods perform feature selection during the model training period. This is the reason why they are called embedded methods. Here the model can perform both feature selection and training at the same time.
Some of the popular methods are-
<ul><li>
 L1 (LASSO) regularization
 </li>
 <li>
 L2(Ridge) regularization
 </li>
 <li>
 decision tree based feature selection</li></ul><h5>Feature Extraction Methods</h5>
This technique tries to reduce the number of features by creating new features from the existing ones. Then it discards the original features. The newly built set of features contain most of the crucial information of the dataset.&nbsp;
Some of the popular feature extraction methods are-
<ul><li>
 <a href="https://www.aionlinecourse.com/tutorial/machine-learning/principal-component-analysis" target="_blank">Principal Component Analysis (PCA)</a>
 </li>
 <li>
 <a href="https://www.aionlinecourse.com/tutorial/machine-learning/linear-discriminant-analysis-%28lda%29" target="_blank">Linear Discriminant Analysis (LDA)</a>
 </li>
 <li>
 <a href="https://www.aionlinecourse.com/tutorial/machine-learning/kernel-pca-in-python" target="_blank">Kernel PCA</a>
 </li>
 <li>
 Quadratic Discriminant Analysis (QDA)
 </li>
</ul>

Dimensionality Reduction

Support Vector regression implements a support vector machine to perform regression. In this tutorial, you'll get a clear understanding of Support Vector Regression in Python.