Kernel SVM for Dummies(with Python Code) | Machine Learning

In this tutorial, we are going to introduce the Kernel Support Vector Machine and how to implement it in Python.

Kernel SVM Intuition:
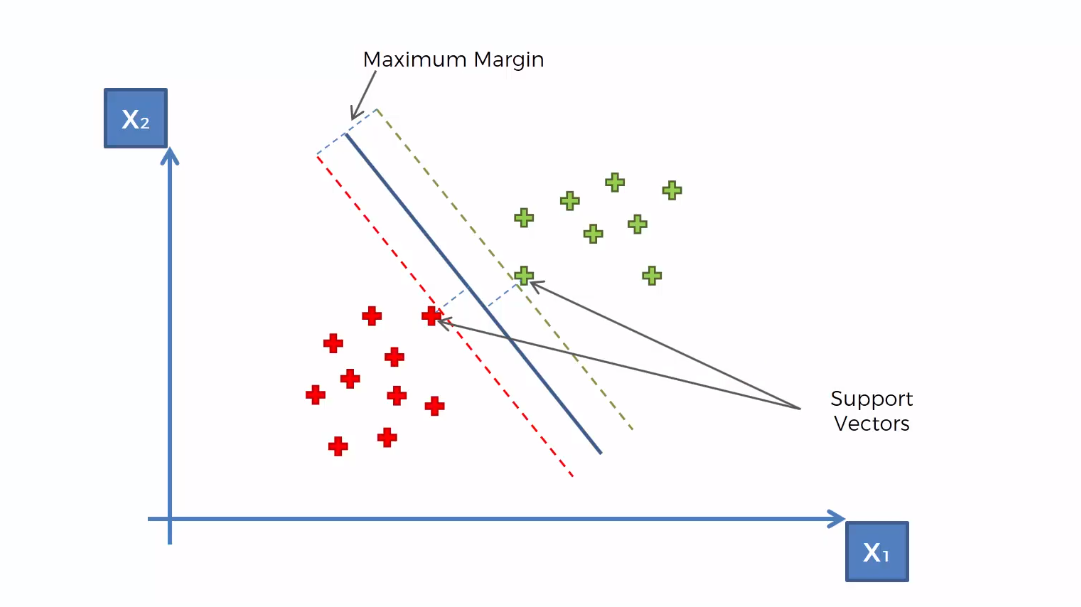
In the previous Support Vector Machine tutorial, we implemented SVM for the following scenario.

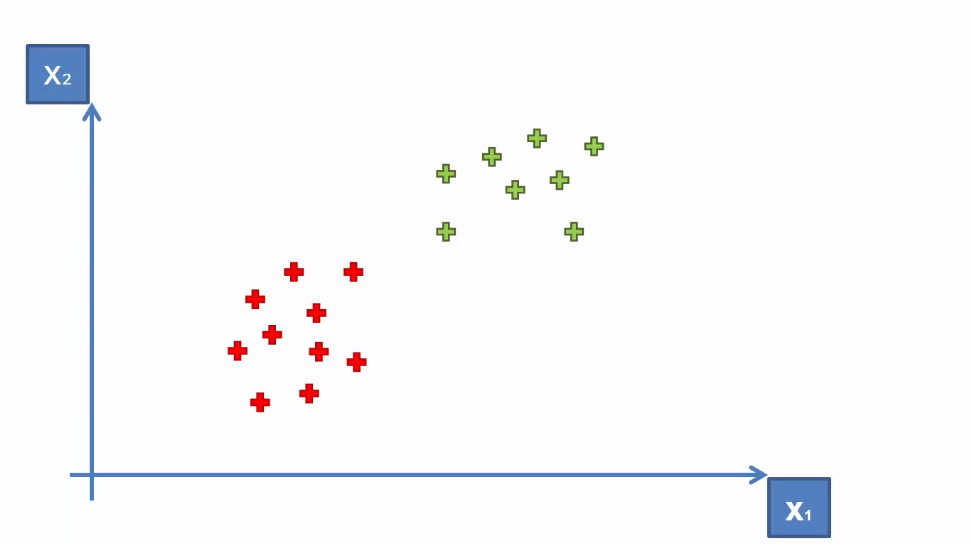
Here the data points are linearly separable. That means we can separate the data points with a straight line.

But what if we have data points like the following

                                

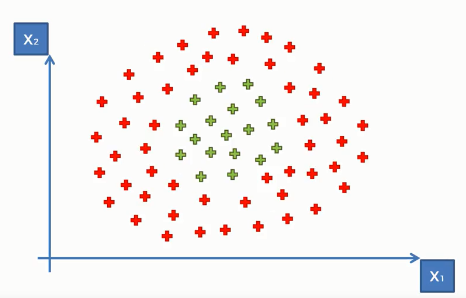
Here the data points do not look like the previous data points(though both in the same dimensional space). As we can see they can not be separated into two distinctive classes with a straight line. This is because these data points are not linearly separable.

So what can we do to make them linearly separable so that we can apply the SVM algorithm to the data point? 

Well, we can do one thing, that is we can take the data points in a higher-dimensional space where they become linearly separable. To get a clear idea of this concept, lets look at the following illustration.

                           

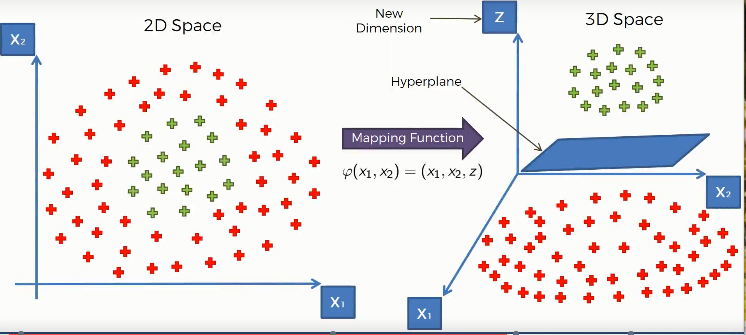
Here we used a mapping function(a function that maps the lower-dimensional data points in a higher-dimensional space), that elevates our data points into a higher dimensional space where they become linearly separable. And we find a hyperplane that classifies the data points into two distinctive classes.

Then we will project our data points to the initial dimensional space using another function.

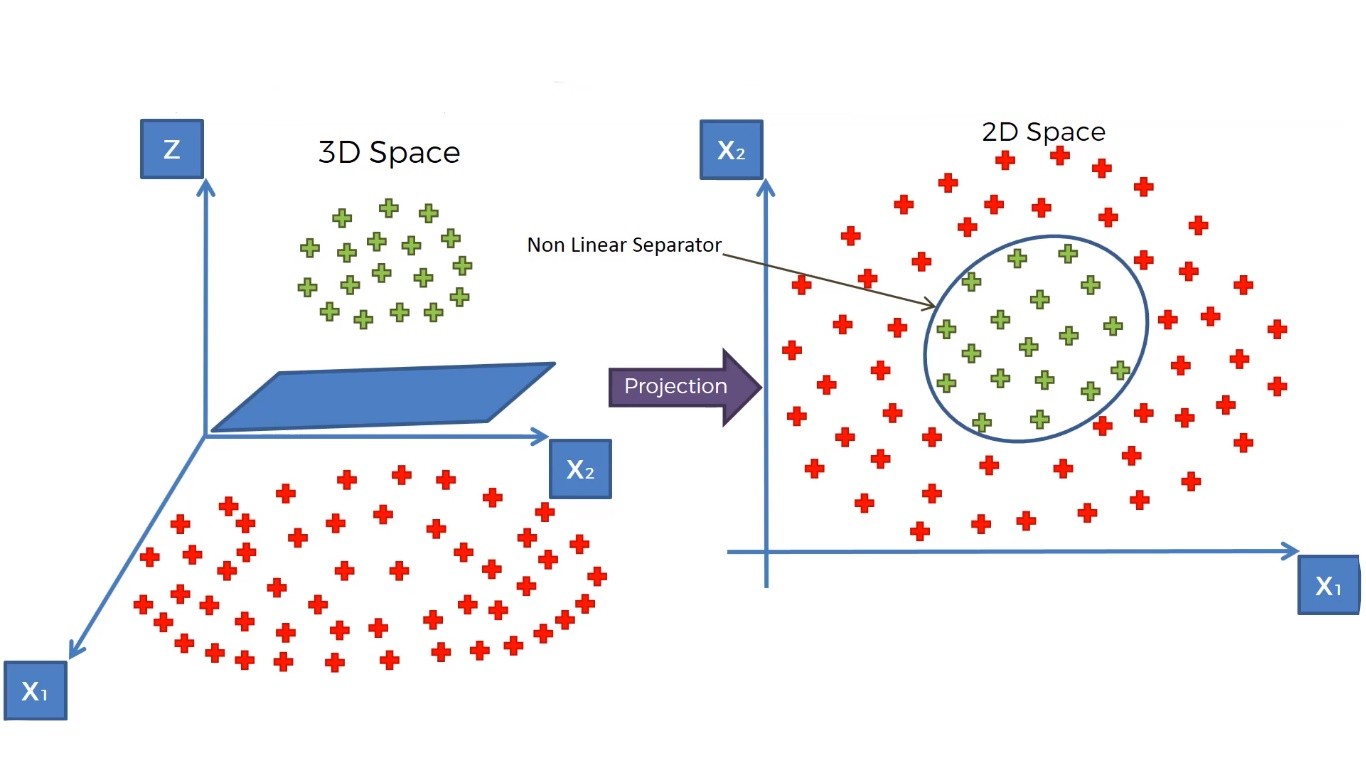
This is the whole idea of separating non-linear data points. In SVM, we do this by a special method or function called Kernel Trick.

In simple terms, Kernel Tricks are functions that apply some complex mathematical operations on the lower-dimensional data points and convert them into higher dimensional space, then find out the process of separating the data points based on the labels and outputs you have defined.

There are many kernel tricks used in SVM. Some most used kernels are- the Gaussian RBF Kernel, Polynomial Kernel, Sigmoid Kernel, etc.

Here we choose the Gaussian RBF Kernel.

The Kernel trick: Here we choose the Gaussian RBF Kernel function.

                          

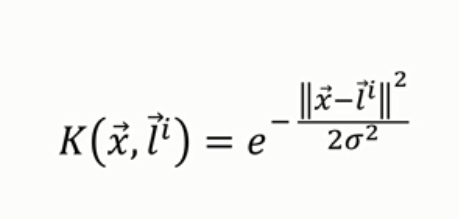
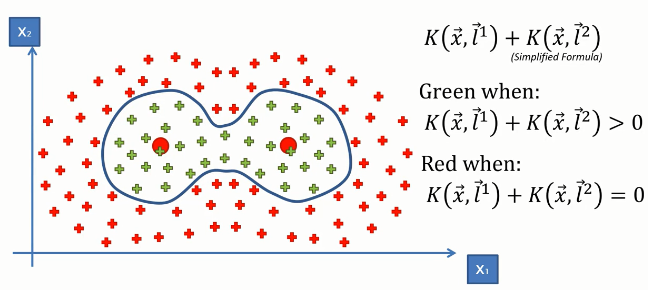
And using the simplified formula of this Kernel Function stated above, we can find the classification of data points like the following.

                       

Kernel SVM in python: Now, we will implement this algorithm in Python. For this task, we will use the Social_Network_Ads.csv dataset. Let's have a glimpse of that dataset.

                                            

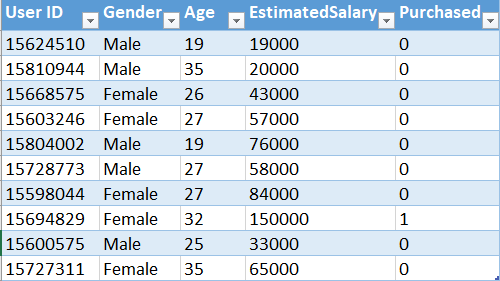
This dataset contains the buying decision of a customer based on gender, age and salary. Now, using SVM, we need to classify this dataset to predict the decision for unknown data points.

You can download the whole dataset from here.

First of all, we need to import essential libraries. You will get the code in Google Colab also.

import numpy as np
import matplotlib.pyplot as plt
import pandas as pd

Then we will import the dataset.

dataset = pd.read_csv('Social_Network_Ads.csv')

Now, let's divide the features of the dataset into feature matrix X and dependent variable vector y.

X = dataset.iloc[:, [2, 3]].values
y = dataset.iloc[:, 4].values

Then we will make training and test sets.

from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.25, random_state = 0)

Let's scale the training and test sets.

from sklearn.preprocessing import StandardScaler
sc = StandardScaler()
X_train = sc.fit_transform(X_train)
X_test = sc.transform(X_test)

It's time to fit SVC into our model. For this, we will use the SVC class from the ScikitLearn library.

from sklearn.svm import SVC
classifier = SVC(kernel = 'rbf', random_state = 0)
classifier.fit(X_train, y_train)

We have built our model. Let's say how it predicts on the test set.

y_pred = classifier.predict(X_test)

We are going to visualize the predicted result.

# Visualising the Test set results
from matplotlib.colors import ListedColormap
X_set, y_set = X_test, y_test
X1, X2 = np.meshgrid(np.arange(start = X_set[:, 0].min() - 1, stop = X_set[:, 0].max() + 1, step = 0.01),
                     np.arange(start = X_set[:, 1].min() - 1, stop = X_set[:, 1].max() + 1, step = 0.01))
plt.contourf(X1, X2, classifier.predict(np.array([X1.ravel(), X2.ravel()]).T).reshape(X1.shape),
             alpha = 0.75, cmap = ListedColormap(('red', 'green')))
plt.xlim(X1.min(), X1.max())
plt.ylim(X2.min(), X2.max())
for i, j in enumerate(np.unique(y_set)):
    plt.scatter(X_set[y_set == j, 0], X_set[y_set == j, 1],
                c = ListedColormap(('red', 'green'))(i), label = j)
plt.title('Kernel SVM (Test set)')
plt.xlabel('Age')
plt.ylabel('Estimated Salary')
plt.legend()
plt.show()

  The above code will generate the following graph.

                        

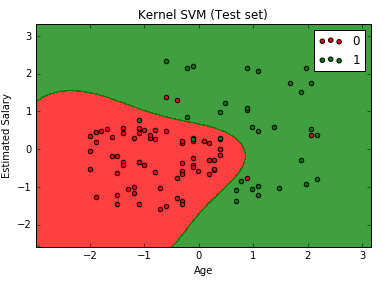
We can see that the graph looks different than that of the previous SVM result. This is because we modeled the data points in a higher-dimensional space.