Dynamic Modeling of Self-Driving Car | Self Driving Cars

The dynamic modeling of a self-driving car refers to how the vehicle operates and reacts dynamically based on the inputs of the autonomous system. To perform the functions of path planning and path tracking, autonomous driving cars must know the vehicle model, such as kinematic or dynamic model. The route tracking results will be better if the vehicle dynamic model is better. To achieve accurate autonomous driving motion control, the autonomous system must select the appropriate variables for exact vehicle motion prediction.

Roles of Dynamic Modeling

To accomplish the objective of autonomy, the roles and responsibilities of a vehicle dynamic modeling in a self-driving system are enormous. Here are a few examples:

• For accurate findings, various tests and test procedures were created and executed.
• Computer simulations are used to ensure driver and passenger safety.
• Contribute ideas and suggestions for bettering the design and performance.
• To comply with all standards and give feedback for improvement, communicate and cooperate with personnel from various departments.

Vehicle Models

The motion of a car on the road is quite complex. One of the helpful techniques for obtaining accurate descriptions of automobile motion is to utilize a complicated system of differential equations with multiple variables describing car motion. The need for real-time performance can be addressed, especially in motion planning, by using linearization and simplification of the vehicle model. The linearization and simplification of automobile models, such as tire elliptical models and point-mass models, are key approaches to solving them.
Some most commonly used vehicle models are given below:

The Kinematic Bicycle Model

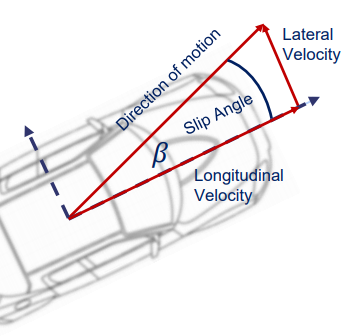
The kinematic bicycle model is a simple model in which we may discover a set of state equations that explain the motion of the vehicle. It can calculate x position, y position, vehicle heading, and steering angle by taking the velocity and rate of change of the steering angle as inputs and computing the outputs using state equations. It used three reference sites on the vehicle to derive these state equations. The front axle, the rear axle, and the center of mass are the three components. Each reference point yields a unique set of state equations, the most significant of which is the center of mass, which allowed us to calculate the vehicle's sideslip angle.
Despite the fact that the kinematic bicycle model is a very simple vehicle model with a lot of assumptions, it is nevertheless an important part of understanding and building a more comprehensive vehicle model. You may now begin to eliminate assumptions from the model and incorporate a more comprehensive understanding of the vehicle dynamics.

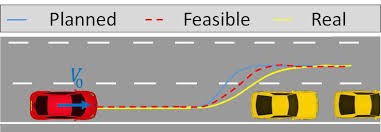
Longitudinal Vehicle Modeling

The vehicle's longitudinal orientation is its forward motion. The forward direction can be seen in two ways: one with respect to the vehicle body itself, and the other with respect to a fixed reference point. When dealing with vehicle acceleration and velocity, the former is frequently employed. When the vehicle's position information in relation to a beginning or finishing point is required, the latter is utilized.

Lateral Vehicle Modeling

Sideways movement of the vehicle is known as lateral movement. There are two methods to look at the lateral direction, one with respect to the vehicle and the other with respect to a fixed reference point. Because high amounts of lateral acceleration or lateral velocity can reduce vehicle stability and controllability, this direction is typically more interesting to researchers than the longitudinal one.

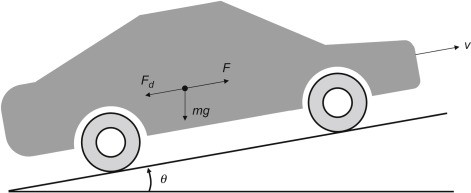
Vehicle Actuation

The most common vehicle actuation systems are throttling braking and steering. The steering angle is the primary input to the lateral dynamics, whereas the throttle pedal position and brake pedal position are the primary inputs to the longitudinal dynamics. These inputs specify some of the forces and moments acting on the vehicle and enter into the ordinary differential equations governing the vehicle's state. It's worth noting that the lateral and longitudinal motions can interact. The vehicle lateral kinematics are then driven by the lateral forces and moments, resulting in a vehicle lateral velocity in desire rate. Vehicle control's primary goal is to give appropriate steering, throttle, and braking signals to maintain the vehicle on track and following a predetermined speed profile.

Tire Slip Modeling

Because the tire is the only component that keeps the vehicle in contact with the road, it is one of the most essential elements in vehicle modeling. This model calculates the resulting forces between the road and the wheels, which Newton's laws utilize to execute the proper vehicle motion. The lateral forces that result will be discussed first, followed by longitudinal forces.
These models determine how much longitudinal and lateral force each tire can handle. The vehicle controller can use this information to calculate what inputs are required for the vehicle to follow a reference trajectory. The influence of tire forces in both the longitudinal and lateral directions at the same time is an essential component of tire modeling. This is crucial information since both forces will be necessary to either follow the supplied trajectory or decide whether the reference trajectory is even achievable.

Conclusion

When creating an autonomous car, having an accurate vehicle dynamic model offers several advantages. One advantage is that it may be used to assess whether a path is feasible or not. Another advantage is that it may be simplified and utilized as a control model. Another advantage is the ability to put the entire model into a simulation environment and properly evaluate how the vehicle will respond in a variety of scenarios. It is considerably easier and safer to do this than to test the car on actual roads.

Thank you for reading the article. For any queries or suggestions, you can feel free to comment below. Your comments are always important to us.